


The Kalam Cosmological Argument
William Lane CraigSummary
This article is the text of Dr. Craig's 2015 lecture at the University of Birmingham, where he did his doctoral studies which led to the revival of the kalam cosmological argument in our day.
As a boy I wondered at the existence of the universe. I wondered where it came from. Did it have a beginning? I remember lying in bed at night trying to think of a beginningless universe. Every event would be preceded by another event, back and back into the past, with no stopping point—or, more accurately, no starting point! An infinite past, with no beginning! My mind reeled at the prospect. It just seemed inconceivable to me. There must have been a beginning at some point, I thought, in order for everything to get started.
Little did I suspect that for centuries—millennia, really—men had grappled with the idea of an infinite past and the question of whether there was a beginning of the universe. Ancient Greek philosophers believed that matter was necessary and uncreated and therefore eternal. God may be responsible for introducing order into the cosmos, but He did not create the universe itself.
This Greek view was in contrast to even more ancient Jewish thought about the subject. Hebrew writers held that the universe has not always existed but was created by God at some point in the past. As the first verse of the Hebrew holy scriptures states: “In the beginning God created the heavens and the earth” (Genesis 1:1).
Eventually these two competing traditions began to interact. There arose within Western philosophy an ongoing debate that lasted for well over a thousand years about whether or not the universe had a beginning. This debate played itself out among Jews and Muslims as well as Christians, both Catholic and Protestant. It finally sputtered to something of an inconclusive end in the thought of the great eighteenth century German philosopher Immanuel Kant. He held, ironically, that there are rationally compelling arguments for both sides, thereby exposing the bankruptcy of reason itself!
I first became aware of this debate only after graduating from university. Wanting to come to terms with this question, I decided upon completion of my Master’s degree work in philosophy to find someone who would be willing to supervise a doctoral thesis on this question. The person who stood out above all others was Prof. John Hick at the Universty of Birmingham. We did come to Birmingham, and I did write on the cosmological argument under Prof. Hick’s direction, and eventually three books flowed out of that doctoral thesis. I was able to explore the historical roots of the argument, as well as deepen and advance the analysis of the argument. I also discovered quite amazing connections to contemporary astronomy and cosmology.
Because of its historic roots in medieval Islamic theology, I christened the argument “the kalam cosmological argument” (“kalam” is the Arabic word for medieval theology). Today this argument, largely forgotten since the time of Kant, is once again back at center stage. The Cambridge Companion to Atheism (2007) reports, “A count of the articles in the philosophy journals shows that more articles have been published about . . . the Kalam argument than have been published about any other . . . contemporary formulation of an argument for God’s existence. . . . theists and atheists alike ‘cannot leave [the] Kalam argument alone’” (p. 183).
What is the argument which has stirred such interest? Let’s allow one of the greatest medieval protagonists in this debate to speak for himself. Al-Ghazali was a twelfth century Muslim theologian from Persia, or modern day Iran. He was concerned that Muslim philosophers of his day were being influenced by ancient Greek philosophy to deny God’s creation of the universe. After thoroughly studying the teachings of these philosophers, Ghazali wrote a withering critique of their views entitled The Incoherence of the Philosophers. In this fascinating book, he argues that the idea of a beginningless universe is absurd. The universe must have a beginning, and since nothing begins to exist without a cause, there must be a transcendent Creator of the universe.
Ghazali formulates his argument very simply: “Every being which begins has a cause for its beginning; now the world is a being which begins; therefore, it possesses a cause for its beginning.” [1]
Ghazali’s reasoning involves three simple steps:
1. Whatever begins to exist has a cause of its beginning.
2. The universe began to exist.
3. Therefore, the universe has a cause of its beginning.
Let’s look at each step of this argument.
Premise 1
Notice that Ghazali does not need a premise so strong as (1) in order for his argument to succeed. The first premise can be more modestly stated.
1'. If the universe began to exist, then the universe has a cause of its beginning.
This more modest version of the first premise will enable us to avoid distractions about whether subatomic particles which are the result of quantum decay processes come into being without a cause. This alleged exception to (1) is irrelevant to (1'). For the universe comprises all contiguous spacetime reality. Therefore, for the whole universe to come into being without a cause is to come into being from nothing, which is absurd. In quantum decay events, the particles do not come into being from nothing. As Christopher Isham, Britain’s premier quantum cosmologist, cautions,
Care is needed when using the word ‘creation’ in a physical context. One familiar example is the creation of elementary particles in an accelerator. However, what occurs in this situation is the conversion of one type of matter into another, with the total amount of energy being preserved in the process. [2]
Thus, this alleged exception to (1) is not an exception to (1').
Let me give three reasons in support of premise (1'):
1. Something cannot come from nothing. To claim that something can come into being from nothing is worse than magic. When a magician pulls a rabbit out of a hat, at least you’ve got the magician, not to mention the hat! But if you deny premise (1'), you’ve got to think that the whole universe just appeared at some point in the past for no reason whatsoever. But nobody sincerely believes that things, say, a horse or an Eskimo village, can just pop into being without a cause.
2. If something can come into being from nothing, then it becomes inexplicable why just anything or everything doesn’t come into being from nothing. Think about it: why don’t bicycles and Beethoven and root beer just pop into being from nothing? Why is it only universes that can come into being from nothing? What makes nothingness so discriminatory? There can’t be anything about nothingness that favors universes, for nothingness doesn’t have any properties. Nor can anything constrain nothingness, for there isn’t anything to be constrained!
3. Common experience and scientific evidence confirm the truth of premise 1'. The science of cosmogeny is based on the assumption that there are causal conditions for the origin of the universe. So it’s hard to understand how anyone committed to modern science could deny that (1') is more plausibly true than false.
So I think that the first premise of the kalam cosmological argument is surely true.
Premise 2
The more controversial premise in the argument is premise 2, that the universe began to exist. This is by no means obvious. Let’s examine both philosophical arguments and scientific evidence in support of premise 2.
First Philosophical Argument
Ghazali argued that if the universe never began to exist, then there has been an infinite number of past events prior to today. But, he argued, an infinite number of things cannot exist. Ghazali recognized that a potentially infinite number of things could exist, but he denied that an actually infinite number of things could exist.
When we say that something is potentially infinite, infinity serves merely as an ideal limit which is never reached. For example, you could divide any finite distance in half, and then into fourths, and then into eighths, and then into sixteenths, and so on to infinity. The number of divisions is potentially infinite, in the sense that you could go on dividing endlessly. But you would never arrive at an “infinitieth” division. You would never have an actually infinite number of parts or divisions.
Now Ghazali has no problem with the existence of merely potential infinites, for these are just ideal limits. But he argued that if an actually infinite number of things could exist, then various absurdities would result. If we’re to avoid these absurdities, then we must deny that an actually infinite number of things exist. That implies that the number of past events cannot be actually infinite. Therefore, the universe cannot be beginningless; rather the universe began to exist.
It’s very frequently alleged that this kind of argument has been invalidated by developments in modern mathematics. In modem set theory the use of actually infinite sets is commonplace. For example, the set of the natural numbers {0, 1, 2, . . .} has an actually infinite number of members in it. The number of members in this set is not merely potentially infinite, according to modern set theory; rather the number of members is actually infinite. Many people have inferred that these developments undermine Ghazali’s argument.
But is that really the case? Modern set theory shows that if you adopt certain axioms and rules, then you can talk about actually infinite collections in a consistent way, without contradicting yourself. All this accomplishes is showing how to set up a certain universe of discourse for talking consistently about actual infinites. But it does absolutely nothing to show that such mathematical entities really exist or that an actually infinite number of things can really exist. If Ghazali is right, then this universe of discourse may be regarded as just a fictional realm, like the world of Sherlock Holmes, or something that exists only in your mind.
The way in which Ghazali brings out the real impossibility of an actually infinite number of things is by imagining what it would be like if such a collection could exist and then drawing out the absurd consequences. Let me share one of my favorite illustrations called “Hilbert’s Hotel,” the brainchild of the great German mathematician David Hilbert.
Hilbert first invites us to imagine an ordinary hotel with a finite number of rooms. Suppose, furthermore, that all the rooms are full. If a new guest shows up at the desk asking for a room, the manager says, “Sorry, all the rooms are full,” and that’s the end of the story.
But now, says Hilbert, let’s imagine a hotel with an infinite number of rooms, and let’s suppose once again that all the rooms are full. This fact must be clearly appreciated. There is not a single vacancy throughout the entire infinite hotel; every room already has a flesh-and-blood person in it. Now suppose a new guest shows up at the front desk, asking for a room. “No problem,” says the manager. He moves the person who was staying in room #1 into room #2, the person who was staying in room #2 into room #3, the person who was staying in room #3 into room #4, and so on to infinity. As a result of these room changes, room #1 now becomes vacant, and the new guest gratefully checks in. But before he arrived, all the rooms were already full!
It gets worse! Let’s now suppose, Hilbert says, that an infinity of new guests shows up at the front desk, asking for rooms. “No problem, no problem!” says the manager. He moves the person who was staying in room #1 into room #2, the person who was staying in room #2 into room #4, the person who was staying in room #3 into room #6, each time moving the person into the room number twice his own. Since any number multiplied by two is an even number, all the guests wind up in even-numbered rooms. As a result, all the odd-numbered rooms become vacant, and the infinity of new guests is easily accommodated. In fact, the manager could do this an infinite number of times and always accommodate infinitely more guests. And yet, before they arrived, all the rooms were already full!
As a student once remarked to me, Hilbert’s Hotel, if it could exist, would have to have a sign posted outside: “No Vacancy (Guests Welcome).” Can such a hotel exist in reality?
Hilbert’s Hotel is absurd. Since nothing hangs on the illustration’s involving a hotel, the argument can be generalized to show that the existence of an actually infinite number of things is absurd.
Sometimes people react to Hilbert’s Hotel by saying that these absurdities result because the concept of infinity is beyond us and we can’t understand it. But this reaction is mistaken and naïve. As I said, infinite set theory is a highly developed and well-understood branch of modern mathematics. The absurdities result because we do understand the nature of the actual infinite. Hilbert was a smart guy, and he knew well how to illustrate the bizarre consequences of the existence of an actually infinite number of things.
Really, the only thing the critic can do at this point is to just bite the bullet and say that a Hilbert’s Hotel is not absurd. Sometimes critics will try to justify this move by saying that if an actual infinite could exist, then such situations are exactly what we should expect. But this response is inadequate. Hilbert would, of course, agree that if an actual infinite could exist, the situation with his imaginary hotel is what we would expect. Otherwise, it wouldn’t be a good illustration! But the question is whether such a hotel is really possible.
So I think Ghazali’s first argument is a good one. It shows that the number of past events must be finite. Therefore, the universe must have had a beginning. We can summarize Ghazali’s argument as follows:
1. An actual infinite cannot exist.
2. An infinite temporal regress of events is an actual infinite.
3. Therefore an infinite temporal regress of events cannot exist.
Second Philosophical Argument
Ghazali has a second, independent argument for the beginning of the universe. The series of past events, Ghazali observes, has been formed by adding one event after another. The series of past events is like a sequence of dominoes falling one after another until the last domino, today, is reached. But, he argues, no series which is formed by adding one member after another can be actually infinite. For you cannot pass through an infinite number of elements one at a time.
This is easy to see in the case of trying to count to infinity. No matter how high you count, there is always an infinity of numbers left to count.
But if you can’t count to infinity, how could you count down from infinity? This would be like someone’s claiming to have counted down all the negative numbers, ending at zero: . . ., -3, -2, -1, 0. This seems crazy. For before he could count 0, he would have to count -1, and before he could count -1, he would have to count -2, and so on, back to infinity. Before any number could be counted an infinity of numbers will have to have been counted first. You just get driven back and back into the past, so that no number could ever be counted.
But then the final domino could never fall if an infinite number of dominoes had to fall first. So today could never be reached. But obviously here we are! This shows that the series of past events must be finite and have a beginning.
Ghazali sought to heighten the impossibility of forming an infinite past by giving illustrations of the absurdities that would result if it could be done. For example, suppose that for every one orbit that Saturn completes around the sun Jupiter completes two. The longer they orbit, the further Saturn falls behind. If they continue to orbit forever, they will approach a limit at which Saturn is infinitely far behind Jupiter. Of course, they will never actually arrive at this limit.
But now turn the story around: suppose Jupiter and Saturn have been orbiting the sun from eternity past. Which will have completed the most orbits? The answer is that the number of their orbits is exactly the same: infinity! (We can’t slip out of this argument by saying that infinity is not a number. In modern mathematics it is a number, the number of elements in the set {0, 1, 2, 3, . . . }.) But that seems absurd, for the longer they orbit, the greater the disparity grows. So how does the number of orbits magically become equal by making them orbit from eternity past?
Another illustration: suppose we meet someone who claims to have been counting down from eternity past and is now finishing: . . . -3, -2, -1, 0! Whew! Why, we may ask, is he just finishing his countdown today? Why didn’t he finish yesterday or the day before? After all, by then an infinite amount of time had already elapsed. So if the man were counting at a rate of one number per second, he’s already had an infinite number of seconds to finish his countdown. He should already be done! In fact, at any point in the past, he has already had infinite time and so should already have finished. But then at no point in the past can we find the man finishing his countdown, which contradicts the hypothesis that he has been counting from eternity.
Alexander Pruss and Robert Koons have recently defended an engaging contemporary version of Ghazali’s argument called the Grim Reaper Paradox. There are infinitely many Grim Reapers (whom we may identify as gods, so as to forestall any physical objections). You are alive at midnight. Grim Reaper 1 will strike you dead at 1:00 a.m. if you are still alive at that time. Grim Reaper 2 will strike you dead at 12:30 a.m. if you are still alive then. Grim Reaper 3 will strike you dead at 12:15 a.m., and so on. Such a situation seems clearly conceivable—given the possibility of an actually infinite number of things—but leads to an impossibility: you cannot survive past midnight, and yet you cannot be killed by any Grim Reaper at any time. Pruss and Koons show how to re-formulate the paradox so that the Grim Reapers are spread out over infinite time rather than over a single hour, for example, by having each Grim Reaper swing his scythe on January 1 of each past year if you have managed to live that long.
These illustrations only strengthen Ghazali’s claim that no series which is formed by adding one member after another can be actually infinite. Since the series of past events has been formed by adding one event after another, it can’t be actually infinite. It must have had a beginning. So we have a second good argument for premise 2, that the universe began to exist. We can summarize this argument as follows:
1. A collection formed by successive addition cannot be an actual infinite.
2. The temporal series of events is a collection formed by successive addition.
3. Therefore, the temporal series of events cannot be an actual infinite.
First Scientific Confirmation
One of the most astonishing developments of modern astronomy, which Ghazali would never have anticipated, is that we now have strong scientific evidence for the beginning of the universe. The first scientific confirmation of the universe’s beginning comes from the expansion of the universe.
All throughout history men have assumed that the universe as a whole was unchanging. Of course, things in the universe were moving about and changing, but the universe itself was just there, so to speak. This was also Albert Einstein’s assumption when he first began to apply his new theory of gravity, called the General Theory of Relativity, to the universe in 1917.
But Einstein found there was something terribly amiss. His equations described a universe which was either blowing up like a balloon or else collapsing in upon itself. During the 1920s the Russian mathematician Alexander Friedman and the Belgian astronomer Georges LeMaître decided to take Einstein’s equations at face value, and as a result they came up independently with models of an expanding universe. In 1929 the American astronomer Edwin Hubble, through tireless observations at Mt. Wilson Observatory, made a startling discovery which verified Friedman and LeMaître’s theory. He found that the light from distant galaxies appeared to be redder than expected. This “red shift” in the light was most plausibly due to the stretching of the light waves as the galaxies are moving away from us. Wherever Hubble trained his telescope in the night sky, he observed this same red-shift in the light from the galaxies. It appeared that we are at the center of a cosmic explosion, and all of the other galaxies are flying away from us at fantastic speeds!
Now according to the Friedman-LeMaître model, we are not really at the center of the universe. Rather an observer in any galaxy will look out and see the other galaxies moving away from him. This is because, according to the theory, it is really space itself which is expanding. The galaxies are actually at rest in space, but they recede from one another as space itself expands.
The Friedman-LeMaître model eventually came to be known as the Big Bang theory. But that name can be misleading. Thinking of the expansion of the universe as a sort of explosion could mislead us into thinking that the galaxies are moving out into a pre-existing, empty space from a central point. That would be a complete misunderstanding of the model. The theory is much more radical than that.
As you trace the expansion of the universe back in time, everything gets closer and closer together. Eventually the distance between any two points in space becomes zero. You can’t get any closer than that! So at that point you’ve reached the boundary of space and time. Space and time cannot be extended any further back than that. It is literally the beginning of space and time.
To get a picture of this we can portray our three-dimensional space as a two-dimensional disk which shrinks as you go back in time (Fig. 2).
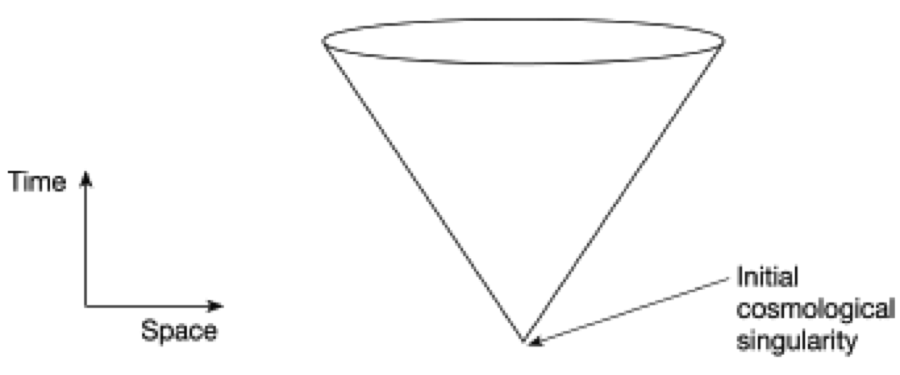
Fig. 2. Geometrical representation of space-time. The two-dimensional disc represents our three-dimensional space. The vertical dimension represents time. As one goes back in time, space shrinks until the distance between any two points is zero. Space-time thus has the geometry of a cone. The point of the cone is the boundary of space and time.
Eventually, the distance between any two points in space becomes zero. So space-time can be represented geometrically as a cone. What’s significant about this is that while a cone can be extended indefinitely in one direction, it has a boundary point in the other direction. Because this direction represents time and the boundary point lies in the past, the model implies that past time is finite and had a beginning.
Because space-time is the arena in which all matter and energy exist, the beginning of space-time is also the beginning of all matter and energy. It’s the beginning of the universe.
Notice that there’s simply nothing prior to the initial boundary of space-time. Let’s not be misled by words. When cosmologists say, “There is nothing prior to the initial boundary,” they do not mean that there is some state of affairs prior to it, and that is a state of nothingness. That would be to treat nothing as though it were something! Rather they mean that at the boundary point, it is false that “There is something prior to this point.”
The standard Big Bang model thus predicts an absolute beginning of the universe. If this model is correct, then we have amazing scientific confirmation of the second premise of the kalam cosmological argument.
So is the model correct, or, more importantly, is it correct in predicting a beginning of the universe? Despite its empirical confimation, the standard Big Bang model will need to be modified in various ways. The model is based, as we’ve seen, on Einstein’s General Theory of Relativity. But Einstein’s theory breaks down when space is shrunk down to sub-atomic proportions. We’ll need to introduce sub-atomic physics at that point, and no one is sure how this is to be done. Moreover, the expansion of the universe is probably not constant, as in the standard model. It’s probably accelerating and may have had a brief moment of super-rapid expansion in the past.
But none of these adjustments need affect the fundamental prediction of the absolute beginning of the universe. Indeed, physicists have proposed scores of alternative models over the decades since Friedman and LeMaître’s work, and those that do not have an absolute beginning have been repeatedly shown to be unworkable. Put more positively, the only viable non-standard models have been those that involve an absolute beginning to the universe. That beginning may or may not involve a beginning point. But on theories (such as Stephen Hawking’s “no boundary” proposal) that do not have a point-like beginning, the past is still finite, not infinite. The universe has not existed forever according to such theories but came into existence, even if it didn’t do so at a sharply defined point.
In a sense, the history of twentieth century cosmology can be seen as a series of one failed attempt after another to avoid the absolute beginning predicted by the standard Big Bang model. That prediction has now stood for nearly 100 years, during a period of enormous advances in observational astronomy and creative theoretical work in astrophysics.
Meanwhile, a series of remarkable singularity theorems has increasingly tightened the loop around empirically tenable models by showing that under more and more generalized conditions, a beginning is inevitable. In 2003 Arvind Borde, Alan Guth, and Alexander Vilenkin were able to show that any universe which is, on average, in a state of cosmic expansion throughout each history cannot be infinite in the past but must have a beginning. That goes for multiverse scenarios, too. In 2012 Vilenkin showed that models which do not meet this one condition still fail for other reasons to avert the beginning of the universe. Vilenkin concluded, “None of these scenarios can actually be past eternal.” [3] “All the evidence we have says that the universe had a beginning.” [4]
The Borde-Guth-Vilenkin theorem proves that classical space-time, under a single, very general condition, cannot be extended to past infinity but must reach a boundary at some time in the finite past. Now either there was something on the other side of that boundary or not. If not, then that boundary just is the beginning of the universe. If there was something on the other side, then it will be a region described by the yet-to-be discovered theory of quantum gravity. In that case, Vilenkin says, it will be the beginning of the universe. Either way, the universe began to exist.
Of course, scientific results are always provisional. We can fully expect that new theories will be proposed, attempting to avoid the universe’s beginning. Such proposals are to be welcomed and tested. Nevertheless, it’s pretty clear which way the evidence points. Today the proponent of Ghazali’s cosmological argument stands comfortably within the scientific mainstream in holding that the universe began to exist.
Second Scientific Argument
As if this weren’t enough, there is actually a second scientific confirmation of the beginning of the universe, this one from the Second Law of Thermodynamics. According to the Second Law, unless energy is being fed into a system, that system will become increasingly disorderly.
Now already in the nineteenth century scientists realized that the Second Law implied a grim prediction for the future of the universe. Given enough time, all the energy in the universe will spread itself out evenly throughout the universe. The universe will become a featureless soup in which no life is possible. Once the universe reaches such a state, no significant further change is possible. It is a state of equilibrium. Scientists called this the “heat death” of the universe.
But this unwelcome prediction raised a further puzzle: if, given enough time, the universe will inevitably stagnate in a state of heat death, then why, if it has existed forever, is it not now in a state of heat death? If in a finite amount of time, the universe will reach equilibrium, then, given infinite past time, it should by now already be in state of equilibrium. But it’s not. We’re in a state of disequilibrium, where energy is still available to be used and the universe has an orderly structure.
The nineteenth century German physicist Ludwig Boltzmann proposed a daring solution to this problem. Boltzmann suggested that perhaps the universe is, in fact, in a state of overall equilibrium. Nevertheless, by chance alone, there will arise more orderly pockets of disequilibrium here and there. Boltzmann refers to these isolated regions of disequilibrium as “worlds.” Our universe just happens to be one of these worlds. Eventually, in accord with the Second Law, it will revert to the overall state of equilibrium.
Contemporary physicists have universally rejected Boltzmann’s daring Many Worlds Hypothesis as an explanation of the observed disequilibrium of the universe. Its fatal flaw is that if our world is just a chance fluctuation from a state of overall equilibrium, then we ought to be observing a much smaller patch of order. Why? Because a small fluctuation from equilibrium is vastly more probable than the huge, sustained fluctuation necessary to create the universe we see, and yet a small fluctuation would be sufficient for our existence. For example, a fluctuation that formed a world no bigger than our solar system would be enough for us to be alive and would be incomprehensibly more likely to occur than a fluctuation that formed the whole universe we see!
In fact, Boltzmann’s hypothesis, if consistently carried out, would lead to a strange sort of illusionism: in all probability we really do inhabit a smaller world, and the stars and the planets we observe are just illusions, mere images on the heavens. For that sort of world is much more probable than a universe which has, in defiance of the Second Law of Thermodynamics, moved away from equilibrium for billions of years to form the universe we observe.
The discovery of the expansion of the universe in the 1920s modified the sort of heat death predicted on the basis of the Second Law, but it didn’t alter the fundamental question. Recent discoveries indicate that the cosmic expansion is actually speeding up. Because the volume of space is increasing so rapidly, the universe actually becomes farther and farther from an equilibrium state in which matter and energy are evenly distributed. But the acceleration of the universe’s expansion only hastens its demise. For now the different regions of the universe become increasingly isolated from one another in space, and each marooned region becomes dark, cold, dilute, and dead. So again, why isn’t our region in such a state if the universe has already existed for infinite time?
The obvious implication of all this is that the question is based on a false assumption, namely, that the universe has existed for infinite time. Today most physicists would say that the matter and energy were simply put into the universe as an initial condition, and the universe has been following the path plotted by the Second Law ever since its beginning a finite time ago.
Of course, attempts have been made to avoid the beginning of the universe predicted on the basis of the Second Law of Thermodynamics. But none of them has been successful. Skeptics might hold out hope that quantum gravity will serve to avert the implications of the Second Law of Thermodynamics. But in 2013, the cosmologist Aron Wall of the University of California was able to formulate a new singularity theorem which seems to close the door on that possibility. Wall shows that, given the validity of the generalized Second Law of Thermodynamics in quantum gravity, the universe must have begun to exist, unless one postulates a reversal of the arrow of time (time runs backwards!) at some point in the past, which, he rightly observes, involves a thermodynamic beginning in time which “would seem to raise the same sorts of philosophical questions that any other sort of beginning in time would.” [5] Wall reports that his results require the validity of only certain basic concepts, so that “it is reasonable to believe that the results will hold in a complete theory of quantum gravity.”
So once again the scientific evidence confirms the truth of the second premise of Ghazali’s cosmological argument.
Conclusion
On the basis, therefore, of both philosophical and scientific evidence, we have good grounds for believing that the universe began to exist. It therefore follows that the universe has a cause of its beginning.
What properties must this cause of the universe possess? This cause must be itself uncaused because we’ve seen that an infinite series of causes is impossible. It is therefore the Uncaused First Cause. It must transcend space and time, since it created space and time. Therefore, it must be immaterial and non-physical. It must be unimaginably powerful, since it created all matter and energy.
Finally, Ghazali argued that this Uncaused First Cause must also be a personal being. It’s the only way to explain how an eternal cause can produce an effect with a beginning like the universe.
Here’s the problem: If a cause is sufficient to produce its effect, then if the cause is there, the effect must be there, too. For example, the cause of water’s freezing is the temperature’s being below 0 degrees Celsius. If the temperature has been below 0 degrees from eternity, then any water around would be frozen from eternity. It would be impossible for the water to begin to freeze just a finite time ago. Now the cause of the universe is permanently there, since it is timeless. So why isn’t the universe permanently there as well? Why did the universe come into being only 14 billion years ago? Why isn’t it as permanent as its cause?
Ghazali maintained that the answer to this problem is that the First Cause must be a personal being endowed with freedom of the will. His creating the universe is a free act which is independent of any prior determining conditions. So his act of creating can be something spontaneous and new. Freedom of the will enables one to get an effect with a beginning from a permanent, timeless cause. Thus, we are brought not merely to a transcendent cause of the universe but to its Personal Creator.
This is admittedly hard for us to imagine. But one way to think about it is to envision God existing alone without the universe as changeless and timeless. His free act of creation is a temporal event simultaneous with the universe’s coming into being. Therefore, God enters into time when He creates the universe. God is thus timeless without the universe and in time with the universe.
Ghazali’s cosmological argument thus gives us powerful grounds for believing in the existence of a beginningless, uncaused, timeless, spaceless, changeless, immaterial, enormously powerful, Personal Creator of the universe.
-
[1]
Al-Gha-zalı-, Kitab al-Iqtisad fi’l-I’tiqad, cited in S. de Beaurecueil, “Gazzali et S. Thomas d’Aquin: Essai sur la preuve de l’exitence de Dieu proposée dans l’Iqtisad et sa comparaison avec les ‘voies’ Thomiste,” Bulletin de l’Institut Francais d’Archaeologie Orientale 46 (1947): 203.
Al-Gha-zalı-, Kitab al-Iqtisad fi’l-I’tiqad, cited in S. de Beaurecueil, “Gazzali et S. Thomas d’Aquin: Essai sur la preuve de l’exitence de Dieu proposée dans l’Iqtisad et sa comparaison avec les ‘voies’ Thomiste,” Bulletin de l’Institut Francais d’Archaeologie Orientale 46 (1947): 203.
-
[2]
Christopher Isham, “Creation of the Universe as a Quantum Process,” p. 378.
Christopher Isham, “Creation of the Universe as a Quantum Process,” p. 378.
-
[3]
Audrey Mithani and Alexander Vilenkin, “Did the universe have a beginning?” arXiv:1204.4658v1 [hep-th] 20 Apr 2012, p. 5. For an accessible video, see see http://www.youtube.com/watch?v=NXCQelhKJ7A (accessed February 23, 2014), where Vilenkin concludes, “there are no models at this time that provide a satisfactory model for a universe without a beginning.”
Audrey Mithani and Alexander Vilenkin, “Did the universe have a beginning?” arXiv:1204.4658v1 [hep-th] 20 Apr 2012, p. 5. For an accessible video, see see http://www.youtube.com/watch?v=NXCQelhKJ7A (accessed February 23, 2014), where Vilenkin concludes, “there are no models at this time that provide a satisfactory model for a universe without a beginning.”
-
[4]
A.Vilenkin, cited in “Why physicists can't avoid a creation event,” by Lisa Grossman, New Scientist (January 11, 2012).
A.Vilenkin, cited in “Why physicists can't avoid a creation event,” by Lisa Grossman, New Scientist (January 11, 2012).
-
[5]
Aron C. Wall, “The Generalized Second Law implies a Quantum Singularity Theorem,” arXiv: 1010.5513v3 [gr-qc] 24 (Jan 2013), p. 38.
Aron C. Wall, “The Generalized Second Law implies a Quantum Singularity Theorem,” arXiv: 1010.5513v3 [gr-qc] 24 (Jan 2013), p. 38.

