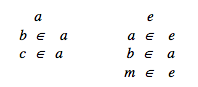God and Abstract Objects

The Theological Challenge of Platonism

            In the prologue of the Gospel of John, the evangelist presents a vision of God as the Creator of all things:  “In the beginning was the Word, and the Word was with God, and the Word was God.   He was in the beginning with God.  All things came into being through him, and without him not one thing came into being” (Jn 1.1-3a).  The evangelist gives us to understand that God through His Word is responsible for the existence of literally everything other than God Himself.  Apart from God every existent belongs to the creaturely realm, the class of things which have come into being (geneta), and so owes its existence to God’s creative Word or Reason (logos), who is later identified as Christ (Jn. 1.14-18).

            Such a doctrine of divine creation can be straightforwardly applied to spatio-temporal entities.  But ever since Plato, philosophers and, subsequently, theologians have struggled to relate the doctrine of creation to a quite different class of entities, known in contemporary parlance as abstract objects.  Usually contrasted with concrete objects, such abstract entities include things like numbers, sets, and other mathematical entities, propositions, and properties.  If such entities exist, they cannot be exempted from being among the things created by God.

            Platonists hold that abstract objects do, indeed, exist as mind-independent entities; anti-Platonists deny that they do.  What reasons might be proffered in support of these rival options?  In the contemporary debate over Platonism, there are principally two arguments lodged against Platonism and one argument in its favor.  The two objections usually urged against Platonism are (i) the epistemological objection and  (ii) the uniqueness objection.[1]  The major consideration weighing in for Platonism is the so-called Indispensability Argument.[2]

            Whether Platonists can successfully defeat the two principal objections lodged against their view may remain a moot question here.  Rather my concern is one that is scarcely ever broached in the philosophical literature:  that Platonism is theologically unacceptable.  If this contention is correct, then, given the truth of theism, it will defeat all forms of Platonism, even versions crafted to avoid the epistemological and uniqueness objections.  Pari passu, if the Indispensability Argument should prove successful in showing Platonism to be true, it would constitute a defeater of classical theism.

            The contemporary debate over Platonism’s theological acceptability was sparked by Alvin Plantinga’s 1980 Aquinas Lecture “Does God Have a Nature?” at Marquette University.[3]  Sharp-sighted critics have observed, however, that Plantinga misconstrued the theological challenge to traditional theism posed by Platonism.[4]  Plantinga argued that the chief difficulty presented by Platonism for traditional theism is the challenge it poses to divine sovereignty; that is to say, if Platonism is true, abstract objects lie outside God’s control.  Plantinga therefore dismisses Nominalism as irrelevant to the discussion, since even if there are no such things as the property of being red, for example, nevertheless it remains necessarily true that whatever is red is colored, and God can do nothing to make it otherwise.  Plantinga is therefore led into chasing rabbits down the trail of universal possibilism, the doctrine that there are no necessary truths.  In the end he opts for a conception of divine sovereignty that does not require everything to be within God’s control. 

            We may—and should—endorse an analysis of omnipotence which does not entail universal possibilism,[5] but the central theological problem posed by Platonism remains unaddressed.  The chief theological failing of Platonism and therefore the reason for its unacceptability for orthodox theists is that Platonism is incompatible with the doctrine of creatio ex nihilo and so fundamentally compromises divine aseity.  For Platonism posits infinite realms of being which are metaphysically necessary and uncreated by God.  The physical universe which has been created by God is an infinitesimal triviality utterly dwarfed by the unspeakable quantity of uncreated beings.  Moreover, the metaphysical pluralism entailed by Platonism’s denial of creatio ex nihilo diminishes God’s aseity.  The divine attribute of existing a se is traditionally understood to be a unique perfection of God, the ens realissimum (ultimate reality).  God alone exists self-sufficiently and independent of all things.  All other beings exist ab alio and are contingent in their being.  By contrast Platonism posits endless infinities of infinities of beings, each of which exists a se not ab alio.  God Himself is reduced to but one being among many.

            The theological challenge posed by Platonism finds its easiest and most obvious solution in Absolute Creationism, which maintains that God has created those abstract objects which exist.[6]  Unfortunately, Absolute Creationism faces two difficulties, the first troublesome and the second truly serious.  First, Absolute Creationism misconstrues either the scope or nature of creation.  From a biblical perspective creation is an inherently temporal concept implying a temporal beginning of existence for any created thing;[7] yet it is plausible that many types of abstract objects, if they exist, exist necessarily and so have no beginning of existence.  So if we think of abstract objects as part of the order of dependent beings existing apart from God, then the scope of creatio ex nihilo becomes miniscule.  The overwhelming bulk of things is merely sustained in being but not, properly speaking, created by God.  If, to avoid this difficulty, we expand the meaning of “creation” so as to make any dependent being the object of God’s creation, then we have radically subverted God’s freedom with respect to creating.  In orthodox Christian thought creation is seen as the freely willed act of God.  He does not create by a necessity of nature, and there are possible worlds in which God refrains from creation and so exists alone.  But Absolute Creationism robs God of His freedom with regard to creating.  The vast majority of being flows from Him with an inexorable necessity independent of His will.  Thus, the ontology of Absolute Creationism is incompatible with the doctrine of creatio ex nihilo, attenuating either God’s freedom or the scope of creation.

The second and more serious problem with Absolute Creationism is that it appears to be logically incoherent.[8]  Simply stated, the problem is that the creation of certain abstract objects presupposes the existence of those objects, so that a vicious explanatory circle is formed.  For example, God cannot create the property of being powerful unless He already has the property of being powerful.[9]  The challenge facing Absolute Creationists is to find a way out of this explanatory circle.[10]  Indeed, I should say that the chief problem posed by the existence of abstract objects to classical theism stems not from their necessary existence but from, in certain cases, their uncreatability.  It is not the existence of abstract objects as such that poses a serious challenge to divine aseity but rather the putative existence of uncreatables.

When the theological challenge posed by Platonism is thus correctly understood, we see that Nominalism, far from being irrelevant, lies at the very heart of the debate, whereas doctrines of divine simplicity and universal possibilism, which preoccupied Plantinga, become of secondary importance.  For if there are no abstract objects, then the challenge posed by Platonism simply evaporates.

            The contemporary debate over Platonism finds its epicenter in the philosophy of mathematics with respect to the ontological status of mathematical objects.  In view of the plethora of alternatives to Platonism about mathematical objects (Fig. 1), Platonists cannot justifiably simply assume that the language of mathematics commits us ontologically to mind-independent abstract entities, especially to such obscure objects as sets. 

On anti-realist views of mathematical objects such as Balaguer’s Fictionalism or Yablo’s Figuralism or Chihara’s Constructibilism or Hellman’s Modal Structuralism, mathematical discourse is not in any way abridged, but there are, notwithstanding, no mathematical objects at all.[11]  The Platonist, then, must provide some argument for the reality of mathematical objects, if he is to maintain that mathematical objects furnish a decisive challenge to the truth of classical theism.

Quine’s Indispensability Argument for Platonism

As alluded to above, about the only argument in favor of Platonism is the so-called Indispensability Argument inspired by W. V. O. Quine.  While confessing a preference for desert ontological landscapes, Quine nevertheless felt obligated to admit mathematical objects, specifically sets, into his ontology because he thought that the truth of our best scientific theories commits us to them.  Remarkably, Quine never articulated or defended this argument at any length, obliging us to reconstruct it as best we can.[12]  Quine’s argument was predicated on several distinctive Quinean theses:

1.  Natural science is the sole arbiter of truth and guide to reality.  (Naturalism)

2.  Statements quantifying over mathematical entities are indispensable to our best, canonically formulated scientific theories.  (Indispensability Thesis)

3.  We are ontologically committed to the values of variables bound by the quantifiers in a first-order symbolization of a true, canonically formulated, scientific statement.  (Criterion of Ontological Commitment)

4.  Confirmation of the truth of our best scientific theories accrues to every indispensable statement of those theories. (Confirmational Holism)

Naturalism ensures that there are no metaphysical or otherwise extra-scientific grounds for rejecting the existence of mathematical objects.  What science alone requires to be real is real, period.  The Indispensability Thesis lies at the heart of every version of the argument.  It is fundamentally the claim that quantification over mathematical entities in our best scientific theories cannot be paraphrased away.  Quine recognizes that statements of ordinary language, if taken prima facie, would involve quantification over pseudo-objects; hence, the need for a canonical formulation of the statements of a scientific theory, ensuring that their ontological commitments are irreducible.  Quine’s Criterion of Ontological Commitment is not a criterion of existence per se but tells us rather what must exist in order for a canonical statement to be true.  Given Naturalism, we shall be ontologically committed only by whatever statements in our best scientific theories are true.  Finally, Confirmational Holism ensures that the indispensable mathematical statements of confirmed scientific theories are themselves true.  For whatever evidence goes to confirm the truth of the theory as a whole goes to confirm every statement it comprises.  Since the mathematical statements of a confirmed scientific theory are true and indispensable, we are ontologically committed by those theories to the mathematical objects quantified over.  Hence, we are required by modern science to believe in the existence of mathematical objects.

            Every one of these Quinean theses is highly controverted, and none of them, much less all of them, is, I think, plausibly true.  Let us say a word about each.

Naturalism

By “Naturalism” in the context of the Indispensability Argument one is not referring to some sort of metaphysical naturalism but rather an epistemological naturalism, or, as Quine put it, naturalized epistemology.[13]  Naturalism in this sense is just “the recognition that it is within science itself, and not in some prior philosophy, that reality is to be identified and described.”[14]  The salient aspect of naturalized epistemology for the Indispensability Argument is its restriction of basic sources of knowledge to the sciences.  If the sciences provide grounds for thinking that abstract objects exist, they cannot be gainsaid because there is no other independent, accepted source of knowledge about reality, in particular no metaphysical or theological arguments that need to be weighed against the deliverances of science. 

No orthodox Christian theist can embrace Quine’s naturalized epistemology, since so doing would exclude divine revelation, along with rational intuition, as a basic source of knowledge about reality.  In weighing Indispensability Arguments for Platonism, Christian theists, in contrast to naturalists, will take seriously the teaching of divine revelation regarding God’s aseity and creatio ex nihilo.  Given the widespread influence of Quine’s naturalized epistemology,[15] the Christian theist will therefore inevitably find himself somewhat out of step with a good deal of contemporary philosophy.  But as Alvin Plantinga has emphasized,[16] the Christian theist does not take his philosophical marching orders from current philosophy, and integrity as Christian thinkers demands that we seek to formulate a worldview that integrates theological knowledge with other basic sources of knowledge such as the natural sciences.  The fact that naturalists reject basic sources of knowledge other than the sciences should not trouble us in our philosophizing.

            Now, of course, as Plantinga acknowledges, if there were some reason to think that our basic sources of knowledge really are restricted to the natural sciences alone, then that would be a genuine matter for concern that would need to be addressed.  But there is no such reason.  Even if we allow that science needs no external justification for its being a basic source of knowledge, there is nothing in science itself that warrants the sweeping claim that there are no extra-scientific basic sources of such knowledge as moral, aesthetic, religious, and metaphysical knowledge.[17]  But then naturalism’s restrictive epistemological stance must be either justified extra-scientifically, which makes naturalism self-defeating, or else be simply unjustified.

Michael Rea argues that naturalism, if it is to be plausible, must be regarded as unjustified.[18]  That is to say, naturalism is most plausibly taken to be a set of methodological dispositions on the part of the inquirer which treats as basic sources of evidence only the deliverances of the natural sciences.  As a set of methodological dispositions (or a research program), naturalism is not a philosophical thesis at all and is therefore neither true nor false.  Since it makes no claims, it requires no justification.  But then neither can it assert its superiority to some other inquirer’s non-naturalistic set of methodological dispositions which treats as basic sources of evidence not only the deliverances of science but, for example, rational intuition or divine revelation. The naturalist may prefer his research program, but he has no grounds for thinking that those who reject his set of methodological dispositions err in doing so.

            Rea calls the views to which one is committed as a result of adopting a certain set of methodological dispositions the “consequences” of one’s research program.[19]  If Quine is right, one of the unwelcome consequences of the naturalistic research program is that one is committed to the reality of abstract objects.  Someone who adopts a different set of methodological dispositions may not, however, find himself so committed, for he may have other, overriding reasons to deny the reality of such objects.  The Christian theist, who rejects as too narrow the basic sources of evidence allowed by the naturalist, cannot be faulted for so doing, unless his own research program should prove to be self-defeating.  The Christian theist thus has extra-scientific, theological grounds for rejecting the reality of uncreated abstract objects.  The rejection of uncreated objects does not automatically disqualify Platonism, since the alternative of Absolute Creationism remains an option to be explored, but the rejection of Naturalism does blunt the force of the Indispensability Argument by allowing theological considerations to be relevant to the question of the reality of abstract objects. The consistent Christian theist who is not an Absolute Creationist will advocate an eliminative nominalism that dismisses the reality of various abstract objects on non-naturalistic, or more specifically, theological, grounds.[20]

Indispensability Thesis

Quine’s Indispensability Thesis flows naturally out of his epistemological naturalism.  On a naturalized epistemology one’s ontology must be derived from the natural sciences.  Reflecting philosophy’s linguistic turn, Quine will turn to language as a guide to ontology, not, indeed, to ordinary language but to a formalized language of science. “The general task which science sets itself is that of specifying how reality ‘really’ is:  the task of delineating the structure of reality as distinct from the structure of one or another traditional language.”[21]

Things are not so simple, however, for even the language of natural science as it now stands is not suitable, in Quine’s view, for disclosing ontological commitments.  The language of science is replete with empty proper names, indexical expressions, tensed verbs, modal vocabulary, quantification over pseudo-entities, and so forth.  Therefore, before the ontological commitments of a scientific theory can be revealed, the theory must be regimented into the canonical sentences of an artificial language.

The most thorough-going linguistic transformation required by Quine is that the sentences of a theory must be recast in the purely extensional language of first-order predicate logic with identity, augmented by the membership relation ε of set theory.[22]  So doing would require a radical re-writing of science to eliminate all intensional contexts, including all modal vocabulary, along with modal logic itself, all tensed and indexical expressions, all doxastic or intentional expressions, and all counterfactual conditionals and reasoning.  Indeed, all sentential connectives apart from the truth-functional connectives “~” and “&” must be removed from scientific theories.[23]

The problem with this proposed regimentation of scientific language, apart from pragmatic concerns, is that Quine provides no reason to think that such a regimentation is even possible, much less desirable, for an empirically adequate science.  Indeed, it seems highly unlikely that such a project could succeed.  Modal notions seem inextricably bound up with science, as is evident, for example, in the use of dispositional terms.  Attempting to de-tense physical science would significantly curtail science’s informativeness about the world, for example, the Big Bang’s marking the beginning of the universe.[24]  Intentional statements would seem to be vital to the human sciences like psychology and sociology, which Quine wants to include among the genuine sciences.  Counterfactual truths are supported by the laws of nature, so that their elimination would cripple science’s explanatory adequacy and predictive ability.  Ironically, Quine’s reformulation of science in purely extensional terms seems no more feasible than the project of a nominalistic de-mathematization of science.

Moreover, the demand that science be cast in the form of first-order logic seems to be no more feasible nor desirable.  Restricting all quantification to universal and existential quantification is far too simplistic.  Generalized Quantifier Theory came to recognize during the 1980s that “all” and “some” belong to a much wider category of quantificational expressions which may be given a unified syntactic and semantic treatment.[25]  These include expressions like “more,” “most,” “many,” “few,” “at least as many as,” “some but no more than five,” “finitely many,” and so on.  Conjoined with nouns, they form quantified noun phrases.  It seems a fantasy to suppose that an empirically adequate science could be re-written so as to prescind from all such quantification.  As a result, the regimented science captured by canonical sentences in standard first-order logical notation will not only be empirically inadequate but will also fail to sanction valid inferences employing such non-standard quantifiers. 

As if the prospects for the success of Quine’s regimentation of science were not already sufficiently gloomy, the situation is made even more grim by Quine’s resort to paraphrase in order to avoid unwanted ontological commitments.  Even canonical scientific sentences may involve us in unwanted ontological commitments through the variables of quantification.  For example, Quine muses that scientific statements could commit us to the existence of units of measure, as in, for example, the sentence “The length of Manhattan is 11 miles.”  Paraphrase can eliminate quantification over and, hence, ontological commitment to units of measure, by re-writing this sentence as “Manhattan’s length-in-miles = 11.”[26]  The paraphrase leaves us committed to the existence of numbers, but not, at least, miles.

The problem with Quine’s requirement of suitable paraphrases to avoid ontological commitment to the values of bound variables lies not in his claim that the language of mathematics is inextricably bound up with that of science.  Despite Hartry Field’s bold attempt to re-write Newtonian physics without utilizing the language of mathematics, most philosophers would agree with Quine that mathematical language cannot be expunged from science.  Rather the difficulty with the requirement of a paraphrase in order to avoid ontological commitment is that Quine provides no algorithm for paraphrasing the sentences of a regimented science into an acceptable form.  Paraphrases must be constructed on an ad hoc, as they come, basis.[27]  As a result we have no guarantee that a regimented science will be able to shed the unwanted and implausible ontological commitments of ordinary language.  Indeed, given the absence of any paraphrastic algorithm, the gerrymandered nature of the paraphrases will permit various paraphrases of the same target sentence quantifying over different objects, so that we do not know what a theory’s ontological commitments are.[28]  In fact, as we shall see below, the ontological relativity which results as a consequence of the plurality of feasible paraphrases seems to be inconsistent with Quine’s notion of ontological commitment.[29]  The hit-or-miss nature of the paraphrastic strategy in the absence of an algorithm also implies that we have no guarantee that nominalistic paraphrases for the mathematical statements featured in scientific theories will not yet be found.  There is nothing in the Indispensability Argument that compels us to decide now, in the absence of an algorithm, whether a sentence quantifying over mathematical objects is susceptible to a nominalistically acceptable paraphrase.  The nominalist could reasonably hold, in the absence of any prescribed procedure for formulating paraphrases, that the desired paraphrases may be feasible but have yet to be discovered.  This is not mere wishful thinking, for there are in fact today nominalistic paraphrases of classical mathematics unknown in Quine’s heyday which have proved to be remarkably successful.[30]

The Achilles Heel of Quine’s Indispensability Thesis, then, is not his claim that mathematical sentences cannot be eliminated from an empirically adequate science.  Rather it is his requirement that as a pre-condition for the employment of his Criterion of Ontological Commitment, the whole of science, including not just the physical but also the human sciences, be re-written in an artificial language which is (i) purely extensional throughout,  (ii) capable of expression in first-order logical notation, and (iii) accompanied by contextual definitions which enable one to paraphrase away implausible ontological commitments.  The idea that such a project is feasible seems little more than a pipe dream.

Criterion of Ontological Commitment

With Quine’s third thesis, his Criterion of Ontological Commitment, we come to the key to his Indispensability Argument for the existence of abstract objects.  Despite the title of his influential essay “On What There Is,” Quine recognized that his criterion is not a criterion of existence but of ontological commitment.[31]  It does not tell us what exists but rather what the proponent of any given theory must regard as existent.  As such the criterion is a metaontological thesis aimed at clarifying ontological disputes.  It reveals the rival ontologies implicit in the disputants’ respective theories.

Quine held that ontological commitment is disclosed through a theory’s variables of quantification:

 

There is no commitment to entities through use of alleged names of them; other things being equal, we can always deny the allegation that the words in question are names.  But still there certainly is commitment to entities through discourse; for we are quite capable of saying in so many words that there are black swans, that there is a mountain more than 8800 meters high, and that there are prime numbers above a hundred.  Saying these things, we also say by implication that there are physical objects and abstract entities; for all the black swans are physical objects and all the prime numbers above a hundred are abstract entities. [32]

Quine did not consider his criterion to be at all controversial.  Indeed, he took it to be “scarcely contestable,” since the meaning of “($x)” is given by the ordinary language locution “there is an object x such that.”[33] 

Unfortunately, things are not so simple.  For Quine was not consistent in the formulation of his criterion, so that it is not as perspicuous as might at first appear.  Sometimes Quine would say, “We may be said to countenance such and such an entity if and only if we regard the range of our variables as including such an entity.  To be is to be a value of a variable.”[34]  But on other occasions he would say, “The entities to which a discourse commits us are the entities over which our variables of quantification have to range in order that the statements affirmed in that discourse be true.”[35]

A moment’s reflection reveals that these formulations do not come to the same thing.  In the first place, it is unclear whether one is ontologically committed to the objects in the domain of one’s quantifiers or to some more restricted collection of objects.  Many of Quine’s formulations suggest that we are ontologically committed to everything in the domain of our quantifiers.  So understanding Quine’s criterion leads to a significantly different ontology than if we take the criterion in a more restricted sense.  For example, if in making a universally quantified statement we intend the domain of the quantifiers to be unrestricted, then we are ontologically committed to literally everything there is—which is hardly informative.  On the other hand, if we take the criterion to commit us only to those objects which must exist if the universally quantified statement is to be true, then we are committed to nothing at all, since universally quantified statements, understood as conditionals, have no existential import and so require no objects in order to be true.  Or again, with respect to existential quantification, if we take as the domain of quantification everything in my backyard, then the statement “There’s a cat in my backyard” commits me ontologically to all the things in my backyard, whereas restricting my ontological commitments only to the things that must exist in order for my statement to be true leaves me committed at most to the existence of a cat.

            Quine later sought to clarify his metaontological posture by distinguishing the ontology of a theory from the ontological commitments of a theory.  In response to Jaakko Hintikka’s comment that “What he [Quine] appears to mean is that a sentence is committed to the existence of all the values of the bound variables it contains, not just to the existence of those specific values (if any) which are needed to make the sentence true,”[36] Quine wrote,

My remaining remark aims at clearing up a not unusual misunderstanding of my use of the term ‘ontic commitment.’  The trouble comes of viewing it as my key ontological term, and therefore identifying the ontology of a theory with the class of all things to which the theory is ontically committed.  This is not my intention.  The ontology is the range of the variables.  Each of the various reinterpretations of the range (while keeping the interpretations of predicates fixed) might be compatible with the theory.  But the theory is ontically committed to an object only if that object is common to all the ranges.[37]

This paragraph is prima facie quite baffling.[38]  Fortunately, another essay published in the same year helps us to understand Quine’s distinction between a theory’s ontology and its ontological commitments.  There Quine explains ontological commitment in terms of a theory’s requiring a specific object to exist:

 

An expression ‘a’ may occur in a theory, we saw, with or without purporting to name an object.  What clinches the matter is rather the quantification ‘($x) (x = a).’  It is the existential quantifier, not the ‘a’ itself, that carries existential import.  This is just what existential quantification is for, of course.  It is a logically regimented rendering of the ‘there is’ idiom.  The bound variable ‘x’ ranges over the universe, and the existential quantification says that at least one of the objects in the universe satisfies the appended condition—in this case the condition of being the object a.  To show that some given object is required in a theory, what we have to show is no more nor less than that that object is required, for the truth of the theory, to be among the values over which the bound variables range.[39]

On this account ontological commitment—what a theory requires to exist—is limited to designated objects.  But what about objects which are not specifically designated?  Most scientific theories are not about designated objects but objects in general of a certain type, for example, fundamental particles of various sorts.  Unless the standard model of particle physics mentions some particular particle, it lacks any ontological commitment to particles.  This may seem strange, given how Quine’s Criterion is normally understood, but it seems to be precisely what Quine affirms:

Our question was:  what objects does a theory require?  Our answer is:  those objects that have to be values of variables for the theory to be true.  Of course a theory may, in this sense, require no objects in particular, and still not tolerate an empty universe either, for the theory might be fulfilled equally by either of two mutually exclusive universes.  If for example the theory implies ‘($x) (x is a dog),’ it will not tolerate an empty universe; still the theory might be fulfilled by a universe that contained collies to the exclusion of spaniels, and also vice versa.  So there is more to be said of a theory, ontologically, than just saying what objects, if any, the theory requires:  we can also ask what various universes would be severally sufficient.  The specific objects required, if any, are the objects common to all those universes.[40]

Here Quine envisions a theory which quantifies existentially over dogs without naming any specific dog.  Such a theory is on his view not ontologically committed to dogs because there is no particular dog which must exist in order for the theory to be true.  Only if a particular dog were the value of a variable in every universe of discourse with respect to which the theory comes out true would the theory require the existence of, or be ontologically committed to, that dog.  But in the case of a theory which is perfectly general there may well be no specific objects which are common to all the universes.  Such a theory would have no ontological commitments at all, no specific objects that are required in order that the theory be true.  That is why Quine insists that there is more to be said of a theory ontologically than what its ontological commitments are.  A theory that quantifies over dogs cannot be true if its universe of discourse is empty, indeed, if there are no dogs.  The ontology of a theory, then, as Quine reminds Hintikka, should not be identified with its ontological commitments.  Its ontology is simply the range of its variables. 

We can see now why Quine should make the initially puzzling assertion that “ontological commitment” is not his key ontological term, despite the widespread misunderstanding that this is Quine’s central metaontological insight.  Since scientific theories are typically general and do not designate specific objects, most scientific theories will have precious few ontological commitments.  Quine’s Criterion of Ontological Commitment, then, was apparently never intended to disclose a theory’s ontology, those entities a given theory assumes to exist.  The ontological commitments of our best scientific theories will be a tiny collection of specifically designated objects like Venus, the Hubble Constant, and Sagittarius (assuming Existential Generalization is applicable in such cases), which is a pale wraith of the ontologies which those theories presuppose. 

Quine’s Criterion of Ontological Commitment thus turns out to be next to useless, since scientific theories have so few ontological commitments.  To find out what a theory assumes to exist, we have to look to the theory’s ontology, not its ontological commitments.  But how do we determine a theory’s ontology?  Quine’s suggestion of identifying a theory’s ontology simply as the range of its bound variables is problematic because of its uninformativeness or arbitrariness.  Some different criterion is needed.

In sum, Quine’s Criterion of Ontological Commitment is pretty clearly flawed.  Any Indispensability Argument with reasonable prospects for success is going to have to feature a more plausible criterion than Quine’s.

Confirmational Holism

In Quine’s view, sentences of scientific theories are not subject to confirmation or disconfirmation by evidence in isolation but only as parts of whole theories.  It is the theory as a whole which is subject to testing, and its component sentences enjoy confirmation or suffer disconfirmation insofar as they share in the confirmation or disconfirmation of the whole.  “Science is a unified structure, and in principle it is the structure as a whole, and not its component statements one by one, that experience confirms or shows to be imperfect.”[41]  Since sentences quantifying over mathematical objects are an ineradicable part of science, it follows that they, like purely empirical sentences, share in the confirmation enjoyed by the theory of which they are a part.

Confirmational holism is vital to Quine’s Indispensability Argument because it forestalls the objection that confirmed scientific theories may include sentences which are not themselves true.  All the sentences of a theory are confirmed by the evidence supporting that theory.  Hence, if the theory is judged to be true on the basis of the evidence, so must be its component sentences having mathematical objects as values of bound variables.  Thus, if we accept a theory as confirmed by the evidence, we are committed to the truth of its mathematical sentences and, hence, committed to the existence of the mathematical objects which are values of their bound variables.

Quine’s Confirmational Holism is, however, a highly implausible and therefore widely rejected doctrine, the least plausible of the four theses comprised by his Indispensability Argument.  Elliott Sober has convincingly exposed its weakness, charging that “The confirmation relation that holism invokes is bizarre.”[42]  Sober importantly distinguishes distributive holism from non-distributive holism.  Quine endorses and his Indispensability Argument requires distributive holism, according to which it is not merely a theory as a whole which enjoys confirmation or suffers disconfirmation, but its individual sentences as parts of the whole:  in virtue of the confirmation of the theory as a whole, each of its several sentences is confirmed.  Distributive holism is a strange doctrine, since confirmation does not seem to be distributive in the way the doctrine envisions.  How is it that the confirmation which a theory as a whole enjoys gets distributed to all its several parts?  Sober reminds us that it is fallacious to infer that because an observation O confirms a hypothesis H and H entails some statement S, therefore O confirms S.  (Let O = the playing card is red; H = the card is the 7 of hearts; and S = the card is a 7.)  Sober thinks that this fallacious inference (which he calls “the special consequence principle”) underlies distributive confirmational holism, for apart from it all one has is a non-distributive holism, according to which the confirmation/disconfirmation of a whole theory is not distributed to its component parts, and hence, to its mathematical statements.

Furthermore, a property of simple examples of confirmation is symmetry:  observation O confirms hypothesis H just in case not-O would disconfirm H.  Yet the sentences of pure mathematics never suffer disconfirmation from different observational outcomes of theory testing.  The calculus that is used in relativity theory, for example, was used in Newtonian theory and did not share in the disconfirmation of the latter.  Since pure mathematical sentences do not suffer disconfirmation but are common to all theories, neither can they be confirmed by observational evidence.[43]

Sober emphasizes that to reject holism is not to adopt the positivistic alternative of testing isolated hypotheses.  Confirmation/ disconfirmation relations are properly three-place relations:  a hypothesis H is confirmed by an observation O relative to background assumptions A.  The shared background assumptions of competing hypotheses are not tested by the observations and therefore are not confirmed/

disconfirmed along with H.  Now the mathematical sentences of science, precisely by being assumed by every scientific theory, belong to the background assumptions of those theories.  The empirical confirmation of those theories therefore does not extend to mathematical sentences.  For logic and mathematics to be tested empirically, one logical or mathematical statement would have to be contrasted to an alternative statement against a background of shared assumptions in such a way that the competing statements make different predictions about observations—which in the vast majority of cases cannot be done.  It follows, then, that the statements of pure mathematics which underlie scientific theories are not tested when these theories are tested and so do not enjoy confirmation as a result of the theory’s confirmation. 

The failure of Confirmational Holism opens the door for Fictionalist versions of nominalism which do not take the mathematical sentences of scientific theories, at least given conventional semantics, to be literally true.

In sum, the traditional Indispensability Argument defended by Quine must be judged a failure.  Every one of its principal theses is in doubt.  It therefore fails to prove that mathematical objects exist and that the classical theist, confronted with the challenge of Platonism, may not reasonably opt for Nominalism.

The Indispensability Argument Redivivus

Even if Quine’s Indispensability Argument fails, however, that is hardly the end of the story.  Some contemporary Platonists have sought to revise the Indispensability Argument, so as to free it from its objectionable Quinean theses.  For example, Burgess and Rosen have recently enunciated what almost appears to be an Indispensability Argument from shame[44]:

 

1.  Standard mathematics abounds in “existence theorems” that appear to assert the existence of mathematical objects and to be true only if such objects exist.

2.  Well-informed scientists and mathematicians—the “experts”—accept these existence theorems in the sense both that they assent verbally to them without conscious silent reservations and that they rely on them in both theoretical and practical contexts.

3.  The existence theorems are not merely accepted by mathematicians but are acceptable by mathematical standards.

4.  The existence theorems really do assert and imply just what they appear to.

5.  To assent verbally to a claim without conscious, silent reservations, to rely on it in both theoretical and practical contexts, just is to believe that it is true.

6.  The existence theorems are not merely acceptable by specifically mathematical standards but are acceptable by more general scientific standards.

7.  There is no philosophical argument powerful enough to override or overrule mathematical and scientific standards of acceptability in the present instance.

8.  Therefore, if nominalism is true, expert opinion is systematically mistaken (from 1, 2, 4, 5).

9.  Therefore, we are justified in believing (to some high degree) in mathematical objects, which is to say we are justified in disbelieving (to the same high degree) nominalism (from 3, 6, 7, 8).

In this more modest argument for Platonism, (7) takes the place of Naturalism, (6) replaces the Indispensability Thesis, (4) substitutes for the Criterion of Ontological Commitment, and Confirmational Holism is abandoned in favor of (5).

            In their earlier work Burgess and Rosen had attempted to divide Nominalists into two camps:  Hermeneutic Nominalists, who try to provide an analysis of what mathematicians and scientists really mean in making mathematical assertions, and Revolutionary Nominalists, who advocate a reform of science to rid it of all apparent reference to mathematical objects.[45] This false dichotomy drew sharp protests from Nominalists who neither presume to know what mathematicians and scientists in general mean by their assertions nor aspire to an impractical and expensive reform of science, but aim merely to defeat the Indispensability Thesis that quantification over mathematical objects is indispensable to science.[46] In offering the present argument, Burgess and Rosen utilize a similar rubric to categorize their opponents.  Nominalists who accept (8) espouse Revolutionary Nominalism; they must reject (6) or (7).  Those who reject (6) are Naturalized Revolutionary Nominalists, while those who accept (6) but reject (7) are Alienated Revolutionary Nominalists.  On the other hand, Nominalists who deny (8) embrace Hermeneutic Nominalism; they must reject (4) or (5).  Those who deny (4) are Content Hermeneutic Nominalists, while those who deny (5) are Attitude Hermeneutic Nominalists.

            It is immediately evident that some Nominalists are going to fall through the cracks of this categorization, namely, those who reject (6) or (7) but are not Revolutionary Nominalists because they also reject (4) or (5).  There is no apparent incoherence in a Nominalism which is too modest to presume to know what supposed Hermeneutic Nominalists claim to know and yet has scientific or philosophical reasons for doubting the existence of mathematical objects; but such a Nominalism is left out of account by Burgess and Rosen’s taxonomy.

            One might also wonder about those who would reject one or more of (1-3).  But Burgess and Rosen take (1-3) to be “scarcely deniable” and so do not even entertain challenges to them.  This might seem odd, as (1) does not at first seem obviously true—do existence theorems, like “There are infinitely many prime numbers,” in fact appear to assert the existence of mathematical objects?  Do such theorems rather not appear to be mere derivations from more fundamental axioms?  And what of “existence axioms,” such as the Axiom of Infinity?

AI.  There exists at least one set Z with the following properties:  (i) Ø Î Z, and (ii) if x Î Z, also {x} Î Z.

Do not such axioms appear to be mere postulates or definitions rather than serious existential assertions?  Later in their article Burgess and Rosen do mention the existence axioms, oddly ignored in (1-3), in considering the following Nominalist challenge:

Mathematicians . . . generally obtain their existence theorems by deduction from previously established results, which ultimately depend on existence axioms.  But such a deduction provides a justification of the theorems only if the axioms are themselves justified . . . . Have the axioms been justified?  Not by the main corps of mathematicians who seldom if ever consider such questions.[47]

Burgess and Rosen do not disagree but, as we shall see, reject the claim that the basic axioms need some sort of positive defense.  Now if the theorems are simply derivations, then the question becomes how we should understand the existence axioms.  Are they really straightforward existence claims?  Doubtless, Burgess and Rosen would say that misgivings of this sort represent reservations about (4), not (1), emphasizing the word “appear” in (1).  Fair enough; but even given such emphasis, is it still correct to say that existence theorems even appear to be true only if mathematical objects exist?  Such a claim goes beyond appearance into philosophical reflection, where it might after all be denied.  At the level of appearance, it seems fair at most to say that these theorems appear to be true.  Whether mathematical objects are a necessary condition of their truth depends on a philosophical inference that goes beyond appearances.

As for (2), one might well balk at the characterization of scientists and mathematicians as “the experts” when it comes to the issue of Platonism, since that question is not a scientific or mathematical but philosophical question.  The average working scientist or mathematician is unlikely to be an expert when it comes to this question.  This is important because when we reach (8), the (Revolutionary) Nominalist is supposed to be thrust into the embarrassing position of saying that expert opinion is systematically mistaken, even though he himself may be vastly better informed on the question than the scientists and mathematicians to whom he is expected to defer.  Of course, (2) stipulates that our scientists and mathematicians are themselves “well-informed.”  But, then, if we are talking about scientists and mathematicians who are well-read in philosophy of mathematics and apprised of the issues in the debate over the ontological status of mathematical objects, how do we know what “silent reservations” they have in assenting verbally to the existence theorems and relying on them?  For example, mathematicians Kasner and Newman caution that “‘Existence’ in the mathematical sense is wholly different from the existence of objects in the physical world.”[48] Similarly, Rotman and Kneebone state that as a creation of the human mind “the Zermelo-Fraenkel universe of sets exists only in a realm of abstract thought ... the ‘universe’ of sets to which the ... theory refers is in no way intended as an abstract model of an existing Universe, but serves merely as the postulated universe of discourse for a certain kind of abstract inquiry.”[49] Alexander Abian advises,

whenever in the Theory of Sets we are confronted with a statement such as there exists a set x whose elements are sets b and c, and there exists a set u whose elements are the sets x, b and m, then we may take this statement as implying that a table such as the following appears as part of the illusory table which describes the Theory of Sets ...

... The above considerations show how we may interpret more concretely the notion of existence in the Theory of Sets. In short if an axiom or a theorem of the Theory of Sets asserts that if certain sets ... exist, then a certain set ... also exists, we shall interpret this as: if certain sets ... are listed in the above illusory table, then a certain set ... must also be listed in the same illusory table.[50]

As for natural scientists, Penelope Maddy reports, “As a rule physicists seem happy to use any mathematics that is convenient and effective, without concern for the mathematical existence assumptions involved.”[51] Given such caveats, it is far from undeniable that well-informed scientists and mathematicians assent verbally to and rely on existence theorems without conscious reservations about ontological commitments.

            As for (3), the mathematical acceptability of the existence theorems has, of course, been challenged by constructivists, so that this premise is again hardly undeniable.

            Waiving these concerns, however, let us ask what justification Burgess and Rosen offer for their crucial (4-7).  Here we find a subtle shifting of the burden of proof to the shoulders of the Nominalist.  For although they offer their argument as “an argument for anti-nominalism,” their aim in doing so is “simply to point out some of the obstacles a compelling case for nominalism would have to overcome.”[52] Rather than offering positive arguments on behalf of (4-7), they challenge the Nominalist’s ability to establish their contradictories.  But to defeat the Indispensability Argument, one need only undercut, not rebut (that is, falsify), one of the argument’s premises.  One need not be a Nominalist of any stripe to be skeptical of the Platonist’s case for (4-7).

            Consider, then, (4).  Burgess and Rosen enjoy needling imagined Content Hermeneutic Nominalists because they have never “published their suggestions in a linguistics journal with evidence such as a linguist without ulterior ontological motives might accept.”[53]  But surely a tu quoque is in order here.  (4) is the claim that mathematical existence theorems should be understood literally, as implying the existence of mathematical objects.  But what “responsible linguistic investigations”[54] published in professional journals of linguistics can Burgess and Rosen cite in support of this Platonistic thesis?  No such evidence in support of (4) is forthcoming.  Whether or not the existence theorems assert and imply the existence of mathematical objects depends not upon the mathematical content of such theorems, which will be given by definitions of the key terms, but upon a semantic theory of existential quantification and reference, matters which lie far beyond the competence of the average mathematician and scientist.  Whether the existence theorems imply the existence of mathematical objects will be relative to the semantic theory one adopts.  And how will the Platonist justify his conviction that theories entailing different commitments are not equally viable alternatives, that only those having Platonistic commitments are viable semantics for such theorems?

            Strangely, Burgess and Rosen seem to give away the store when, in response to the Nominalistic claim that the statement

            B.  “There exist numbers”

is ontologically innocent because all it really means is

            B*.  There could have been numerals,

they rejoin, “But to concede (B) . . . is to concede all the anti-nominalist maintains [Alston 1958].”[55]  This response is odd, for if (B) means (B*), then, as Alston argues, (B) has no more ontological commitments than (B*).  Thus, the argument for Platonism from mathematical existence theorems collapses.  All linguistic analysis tells us is that (B) and (B*) have the same ontological commitments, but it does not reveal to us what they are.[56]  (B) is thus not shown to be ontologically committing to abstract objects.  Far from being all that the anti-Nominalist maintains, this is all that the Nominalist could ask for.

            What about the warrant for (5)?  Attitude Hermeneutic Nominalism challenges the Platonist to prove that the majority of mathematicians and scientists, in giving verbal assent to and relying on mathematical existence theorems, really believe that there are mathematical objects such as the Platonist asserts there are.  Here again, it is Burgess and Rosen’s responsibility to cite credible sociological surveys published in professional journals describing the attitudes prevalent among professors of mathematics and natural science.  Again, none is forthcoming.

            Burgess and Rosen note that we lack the best kind of direct evidence that the practice of mathematics and science involves something less than belief in existence theorems, namely, efforts to disavow such belief, warning students against believing, and so on.  But such insouciance is consistent with an attitude of indifference toward such metaphysical conundrums—“We’ll leave that question to the philosophers!”—or with the conviction that such theorems can be true without making ontological commitments.  Since it just does not mater to mathematical or scientific practice whether mathematical objects exist, practitioners simply have no incentive to be bothered about them—unless, of course, they have taken a class in philosophy of mathematics, in which case well-informed practitioners may well be skeptical about either the truth of the existence theorems or else the ontological commitments of such truths.  We need a sociological study to tell.

            Burgess and Rosen do acknowledge indirect evidence in favor of the view that practitioners have less than belief in mathematical objects, namely, the lightheartedness with which novel mathematical entities are introduced, the indifference when it comes to questions of identifying mathematical objects such as the number 2 with other objects such as {{Ø}} or {0, 1}, and the varying reactions of mathematicians when pressed by philosophers about the ontological commitments of their theorems.  Pace Burgess and Rosen, these do seem to supply strong grounds for suspecting that statements of mathematical existence are often not understood by mathematicians and scientists as equivalent to the sense in which it is true to say that the Eiffel Tower exists. 

Burgess and Rosen’s attempts to weaken this evidence by speculating about possible alternative explanations for these phenomena are not merely conjectural but implausible.  For example, the lightheartedness with which new mathematical entities are introduced is said to be explained by the fact that assurance of their consistency is generally provided by describing models consisting of already recognized objects, so that the new entities, being identifiable with the recognized objects, may not really be new after all—as if the lightheartedness with which Hilbert space is introduced were not due to its mere instrumental utility but to its being identifiable with a set of points, which are already recognized entities!  Or again, the indifference about identity questions is ascribed to mathematicians’ taking mathematical statements to be statements about positions in structures rather than objects that occupy these positions—as if all mathematicians are and have for a long time been structuralists (and ante rem structuralists at that)!  Again, the varying reactions to philosophical questions is compared to the bewilderment an ordinary person feels when called upon to defend his belief that “I am awake”—as if ordinary people doubt that they are awake, as mathematicians express doubt about whether the number 2 exists (or do not know what to say about it)!  Burgess and Rosen have not merely failed to provide positive evidence for (5) but have not provided adequate defeaters of its defeaters.

            In sum, Burgess and Rosen’s Content and Attitude Hermeneutic Nominalists are straw men, erected to distract attention from their own lack of positive argument on behalf of (4) and (5) of their anti-Nominalist argument.  One need not presume to know, apart form linguistic and sociological studies, whether mathematical existence theorems really imply what they appear to or whether mathematicians and scientists generally believe that they do in order to be justifiably sceptical that the Platonist has proven (4) and (5) to be true. 

            What, then, shall we say of (6) and (7)?  Again, we see the attempt to shift the burden of proof to the imagined Revolutionary Nominalist, who is called upon to falsify these premises.  What is wanted, rather, is some positive argument from the Platonist on behalf of (6) and (7).

            Instead of providing an argument for (6), Burgess and Rosen consider what they call “the ‘dispensability argument’ for nominalism.”[57] The claim is that a good scientific reason for rejecting a theory that purports to describe a special domain of objects is the demonstration that we can construct an alternative theory without such commitments that does all the work of the original theory.  Nominalists like Field, Chihara, and Hellman claim to offer such nominalistic alternatives.  Burgess and Rosen’s complaint is that these alternatives are significantly less perspicuous, tractable, familiar, and fruitful for the further development of science.

            Such a complaint would be significant only if the supposed revolutionaries were proposing their alternative formulations as replacements for current theories.  But they are not.  None of them is advocating a scientific revolution in the name of Nominalism.  If we assume (4), which is moot, these Nominalists are at most committed to saying that current scientific theories are on the whole false, even if their Nominalistic content is true.  But in light of their familiarity, utility, and so forth, we should go right on using the standard theories, while recognizing that we are not committed by them to mathematical objects.

            Burgess and Rosen interpret such Nominalists to claim that avoiding ontological commitment to mathematical objects outweighs the drawbacks of being less perspicuous, tractable, familiar, and so on.  They question whether this consideration counts more than the drawbacks by scientific standards.  Citing Maddy, they observe that historically, scientific theorists have been glad to proliferate mathematicalia.  The revolutionaries are really promoting a philosophical standard of evaluation and therefore are not, after all, Naturalized Revolutionary Nominalists.

            Again, however, Burgess and Rosen misrepresent these Nominalist thinkers.  Since Nominalists are not advocating replacement of standard theories by Nominalistic alternatives, they are not claiming that the admitted drawbacks of their formulations are outweighed by their fewer ontological commitments.  Their claim is at most that the current theories, if taken prima facie, employ useful fictions and that we are not committed to the reality of these fictitious objects, since they are dispensable in light of alternative readings.  Whether their objection to the prima facie reading of current theories is scientific or philosophical is difficult to answer because Burgess and Rosen provide no guidelines for what are scientific and what are philosophical standards of evaluation.  Indeed, given a naturalized epistemology, it is difficult to make sense of such a bifurcation, since philosophy is supposed to be a part of science.  For the naturalist, philosophical concerns about ontological economy will be broadly scientific.  Maddy’s point about natural science’s cordiality toward new mathematical tools was precisely the reason she abandoned realism in favor of anti-realism.  If scientists thought that in adopting new mathematical apparatus, they were actually populating the world with entities as real as a new species of kangaroo or a hitherto unknown planetary system, then such proliferation of real entities would surely be a legitimate scientific concern and arouse serious scientific misgivings.  In short, Burgess and Rosen have not only failed to argue for the truth of (6), under the assumption that the existence theorems are to be construed as ontologically committing, but they have not even refuted the dispensability argument against the broadly scientific acceptability of those theorems so construed.

             Finally, we come to (7).  That those who reject (7) are classed as “alienated” while those who accept it are “naturalized” shows how close beneath the surface Quine’s naturalized epistemology is lurking.  Those who propound philosophical arguments against Platonism are marginalized, excluded from the fashionable in-crowd of scientific naturalists.  Since, as we have seen, scientific naturalism is merely a methodological disposition to accept certain kinds of evidence, is there anything more serious than being unfashionable about not adopting scientific naturalism?  Burgess and Rosen complain, “it is very difficult to settle issues when one rejects scientific standards for settling them.  Argumentation over epistemology (or almost anything else) from an alienated, extra scientific, as opposed to a naturalized, intrascientific, standpoint usually tends to be inconclusive and often tends to bog down in issues of burden of proof.”[58] Such a complaint prizes easy answers over truth.  One might agree that questions may be more solvable when one’s basic sources of evidence are limited to the deliverances of natural science but be unwilling to purchase a solution at the expense of truth.  Prizers of truth may well be willing to live with inconclusiveness and stalemate if that result is avoidable only by a personal choice to restrict what counts as evidence.  In point of fact, this debate has already bogged down in issues of burden of proof, as Burgess and Rosen, rather than supporting their premises, resort to constructing imaginary Hermeneutic and Revolutionary Nominalists and demanding of them proof of the falsity of these premises.

            Now Burgess and Rosen could support (7) as it stands simply by refuting all the philosophical arguments against Platonism, rather than by embracing naturalized epistemology.  So consider their response to the concern of many Nominalists that it is hard to see how we could have knowledge of all these abstracta beyond time and space, causally cut off from us.  The Nominalist will want to know how we can have genuine knowledge of a realm of objects existing in such splendid isolation.  Burgess and Rosen’s response is to compare mathematical knowledge with perceptual knowledge.  We do not know how to show that our perceptual beliefs are true.  Nevertheless, we take them for granted until we are given some sort of positive reason to doubt them.  Similarly, the Platonist may simply reject the Nominalist demand that our basic mathematical assumptions require some sort of positive defense.

            There are a number of problems with this analogy.  First, as Plantinga has emphasized, beliefs which are properly basic need to be grounded in some way.[59] Our perceptual beliefs are grounded in the appearances of things to us.  But in the case of mathematical objects it is their causal inertness that precludes any experience of such objects.  Any sort of appearance of such objects must be akin to a hallucination.  The Platonist might say that while we have no appearances of such entities, nevertheless there is the appearance of self-evidence of the existence axioms of mathematics, which entails their existence.  (N.B. that this would be to abandon naturalized epistemology.)  But the difficulty with this response is not merely that the existence axioms of set theory are generally regarded as not self-evident (one reason for the failure of Logicism), but more importantly—and this leads to the second problem—it is far from self-evident that the truth of the existence axioms implies the existence of mathematical objects.  Burgess and Rosen respond to Yablo’s Figuralism by saying,

Certainly in all clear cases of figurative language—and it is worth stressing that the boundary between figurative and literal is as fuzzy as can be—the non-literal character of the linguistic performance will be perfectly obvious as soon as the speaker is forced to turn attention to the question of whether the remark was meant literally.

            We further submit that mathematical discourse fails this test for non-literalness.[60]

One is tempted to ask what responsible linguistic studies published in professional journals can be cited in support of their opening contention, but never mind.  The more important point is that this objection, if sound, at best proves that mathematical discourse is not a clear case of figurative language, a hardly surprising result.  What does not follow is that mathematical discourse does not lie somewhere in that fuzzy area between clearly figurative and clearly literal expressions.  But if the self-evidence of existence axioms and their derivations is to ground the proper basicality of belief in mathematical objects, then it must be obvious that “There are infinitely many primes” is meant to be taken literally.  Thirdly, in the case of belief in mathematical objects, we have what we do not in general have for perceptual beliefs, namely, a putative undercutting defeater of the belief.  Were we given good reason to believe, say, that we have been dreaming or insane or hallucinating, then our previous perceptual beliefs would no longer be properly basic for us.  Fortunately, we have in general no such defeater for our present perceptual judgements.  But in the case of mathematical objects, it is precisely their causal isolation which does constitute a putative undercutting defeater of those beliefs.  What is wanted now from the Platonist is a defeater-defeater; it is insufficient to re-assert the proper basicality of existence axioms.  Finally, although Plantinga defends the proper basicality and a priori knowledge of mathematical truths, he does so only on the basis of a rejection of Platonism in favor of a thorough-going Conceptualism, according to which no abstract objects exist.

            Whatever we make of the epistemological objection to Platonism, Burgess and Rosen have not shown that there is no philosophical (or theological) argument powerful enough to warrant scepticism about mathematical objects despite their putative acceptability on mathematical and scientific standards. [61]  They themselves admit that once we allow such argumentation into the discussion, the end result will be inconclusive.

Conclusion

            Burgess and Rosen have thus been no more successful than Quine in establishing the key theses of their Indispensability Argument for Platonism.  The abundance of Nominalist defeaters of those theses leaves the issue of the ontological status of mathematical entities at least an open question and various Nominalisms (not to speak of Conceptualism) as viable alternatives to be explored.  The classical theist, committed as he is to divine aseity and creatio ex nihilo, will welcome these alternatives as more compatible with his commitments than is Platonism.

NOTES

• [1]

  Permission has been granted by the University of Notre Dame Press for use of this article. To learn more about the book, please see University of Notre Dame Press site at http://undpress.nd.edu and the webpage for the book at http://undpress.nd.edu/books/P03171.

  Permission has been granted by the University of Notre Dame Press for use of this article. To learn more about the book, please see University of Notre Dame Press site at http://undpress.nd.edu and the webpage for the book at http://undpress.nd.edu/books/P03171.