J. Howard Sobel on the Kalam Cosmological Argument

Introduction

J. Howard Sobel devotes seventy pages of his wide-ranging analysis of theistic arguments to a critique of the cosmological argument. [1] The focus of that critique falls on the argument a contingentia mundi; but he also offers in passing some criticisms of the argument ab initio mundi, or the kalam cosmological argument.

Sobel provides the following statement of the argument:

Sobel will accept the causal premiss (1) only if “begins to exist” means “has a first instant of its existence,” and he disputes the arguments and evidence for (2).

Traditional proponents of the kalam argument sought to justify (2) by means of philosophical arguments against the infinity of the past, while contemporary interest in the argument arises from the empirical evidence of physical cosmology for the truth of (2). Both of these considerations arise in the course of Sobel’s discussion of the possibility of an infinite temporal regress of events, as he weighs Thomas Aquinas’ dictum that “in efficient causes it is not possible to go to infinity”. [3] Now, as Sobel recognizes, Aquinas applied that dictum only to simultaneous, essentially ordered causes, not to temporally successive, accidentally ordered causes. Nonetheless, Sobel considers whether Aquinas should have rejected the possibility of an infinite past on the basis of Thomas’s own arguments against an infinite causal regress.

Mathematical Finitism

Consider, first, Aquinas’ rejection of the possibility of an infinite multitude. If an actually infinite number of things cannot exist, then it would seem that there cannot have been an actually infinite number of past causes. [4] Aquinas rejected the possibility of an infinite multitude because multitudes are differentiated by numbers, and there are no infinite numbers. He argues, “Now the species of multitude are to be reckoned by the species of numbers. But no species of number is infinite; for every number is multitude measured by one. Hence, it is impossible for there to be an actually infinite multitude . . . .” [5] Here Aquinas seems to take an intuitionist line: the reason there are no infinite multitudes in actuality is because there are no infinite numbers. Aquinas appears to deny even mathematical existence to the infinite, countenancing only the natural numbers constructed by mathematical induction.

Sobel’s response to this argument is curious. He waves aside Rudy Rucker’s Cantorian response that there are, in fact, infinite numbers by means of which various multitudes can be distinguished (perhaps realizing, pace Rucker, that Aquinas’ constructivist challenge cannot be met by merely “exhibiting a theory of infinite numbers” [6]. Instead, Sobel attacks the claim that associated with every multitude is a number. He wants to say that there can be real multitudes of things with which no number is associated. He writes,

This passage is not exactly limpid. Charity demands, I think, that we understand the sentence “The species of multitude are not necessarily reckoned by the species of number” to be, not the conclusion of what has gone before, but the commencement of a new thought and, hence, in effect the topic sentence of a new paragraph. Otherwise, first, the sentence reduces to the banal assertion that not all multitudes are reckoned by the natural numbers; and, second, for an example of a multitude beyond number Sobel would need look no further than infinite collections having a cardinal number ℵ0. According to my proposed interpretation, Sobel in the sentence in question has reverted to using the word “number” in the customary way despite his just previously proposed re-definition of the word.

So in his opening remarks Sobel wants to show that infinite multitudes remain as multitudinous even if we agree to use the word “number” as a synonym for “natural number.” Unfortunately, Sobel seems to confuse Aquinas’ mathematico-metaphysical claim that there are no infinite numbers with some sort of stricture on the use of words. We can re-define “number” to mean “natural number” if we want to, and then we and Aquinas would agree that there is no “number” associated with an infinite multitude. But, Aquinas would insist, there would still be associated with such a multitude a measure of its quantity that we used to call a number. Thus, Sobel’s exclamation that the erstwhile infinite multitude, while now not associated with a number, remains just as multitudinous signals a hollow victory. “Of course, it remains as multitudinous,” Aquinas would retort. “And given your re-definition, there is no ‘number’ associated with it. But, then, what’s in a name? What we used to call numbers I’ll call ‘schnumbers.’ So the species of multitude are to be reckoned by schnumbers, one species of which is what you have chosen to call ‘numbers,’ which reckon finite multitudes.” The original mathematico-metaphysical question still remains: are there infinite numbers? Mathematicians sharing Aquinas’ intuitionist bent will say, No, and Aquinas will conclude that there are, therefore, no infinite multitudes in actuality.

So now we come to Sobel’s more significant claim that multitudes are not necessarily associated with numbers in the usual sense of the word “number.” It is odd that he asserts that whether the possibility of a multitude beyond number is realized depends on what multitudes there are and what numbers there are. For that seems to contradict his intended conclusion that we must look for an argument against infinite multitudes “that does not run in terms of what kinds of numbers there are and are not.”[8] It was precisely Aquinas’ contention that what multitudes there are depends on what numbers there are. In any case, Sobel’s only argument for his claim is the appeal to Cantor’s notion of absolute or inconsistent infinities. [9] Sobel has reference here to the possibility of multitudes outside the cumulative type structure explored by set theorists. Classes such as the class of all ordinal numbers or of all sets are not technically sets, since they give rise to the antimonies of naive set theory, but are nonetheless multitudes. Moreover, they are not numbered, since numbers are analyzable in terms of sets, and not all classes are sets.

The problem with this appeal to classes is that no intuitionist who rejects infinite set theory will acquiesce to postulating the existence of transnumerical classes either. If there are not even an infinite number of ordinals, then there is hardly a class of them beyond numbering. It is not sufficient for Sobel merely to assert the existence of such classes in order to chase the intuitionist or Thomist from the field.

Sobel, however, believes that he has a decisive counterexample to the claim that no infinite multitudes exist, namely, the natural numbers themselves. “There are no prospects for persuasive demonstrations of the impossibility of actually infinite multitudes, for there are the infinitely many numbers 1, 2, 3, and so on, there is this ‘many,’ which it is so easy to term a ‘multitude’.” [10] Not only does this assertion beg the question against intuitionistic denials of the mathematical existence of the actual infinite, but, more seriously, it begs the question against non-Platonist views of the ontology of mathematical objects. These are distinct questions, and most non-Platonists would not go to the intuitionistic extreme of denying mathematical legitimacy to the actual infinite; they would simply insist that acceptance of the mathematical existence of certain entities does not imply an ontological commitment to the metaphysical reality of such objects.

Although he does not treat the metaphysical question directly, it is evident in a number of places in his book that Sobel is operating on the presumption of Platonism. For example, in discussing the ontological argument Sobel asserts, “there are things that exist necessarily. For example, the number 23: it is necessary that there exists a prime number greater than 20 and less than 25, and it is 23.” [11] Or again, in denying God’s putative necessary existence, Sobel endorses a quasi-inductive argument relying on the premiss “all the (relatively) uncontroversial examples of necessary objects are abstract,” [12] adding “All relatively uncontroversial examples of necessary things are [eternal]. For example, the number 4 exists ‘timelessly’— ‘exists’ when predicated of it is not in the ‘present temporal tense’.” [13] It is evident that Sobel accepts a Platonist view of mathematical objects as abstract entities existing necessarily beyond time and space.

What remains unclear is Sobel’s justification for so controversial an assumption. In face of the plethora of alternatives to Platonism (Fig. 1), Sobel’s counterexample begs the question. For the proponent of the kalam cosmological argument offers independent arguments against the existence of infinite multitudes of any sort. Sobel’s appeal to mathematical objects as a counter-example is intended to serve as a rebutting defeater of this claim. [14] In order to defeat the alleged defeater, the proponent of the kalam argument need only offer an undercutting defeater of the alleged defeater, that is to say, he need only show that the putative counter-example has not been shown to be a bona fide counter-example, since there are many other viable ways of understanding mathematical existence apart from Platonism.

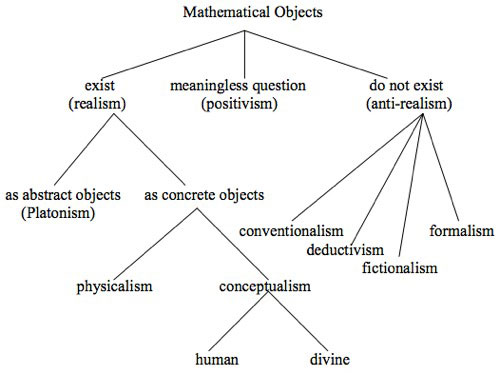
Fig. 1: Various metaphysical options concerning the existence of abstract objects.

For example, on anti-realist views of mathematical objects such as Balaguer’s Fictionalism or Chihara’s Constructibilism there are no mathematical objects at all, let alone an infinite number of them. Interestingly, not even Realism commits one to an actually infinite number of mathematical objects if the concrete realm is finite or the conceptual realm progressively realized in tensed time. Platonic Realism alone seems to entail ontological commitment to an actually infinite multitude of beings. It is ironic that Sobel should be so painstaking and cautious when evaluating theism, yet so cavalier and uncritical when it comes to embracing the sweeping metaphysical commitments of Platonism. Perhaps this differential treatment is justified in view of the greater existential import of theism. At any rate, appeals to mathematical counterexamples as proof that actually infinite multitudes exist are specious apart from a rigorous defense of Platonism to the exclusion of its rivals.

Impossibility of an Infinite Multitude of Past Causes

Turning from the general question of whether infinite multitudes exist, Sobel next examines specific cases to see whether the supposition of an actually infinite multitude “leads ... to a contradiction or ‘evident absurdity’.” [15] The distinction between a contradiction and an absurdity is noteworthy, for something may be absurd without involving logical inconsistency. Sobel himself believes that certain types of infinite causal regresses are really impossible (namely, those involving simultaneous, essentially ordered causes) even though there is no logical inconsistency involved in such series. [16] Is the existence of an actually infinite temporal regress of accidentally ordered causes similarly absurd?

Sobel considers an argument against such a regress from Galileo, which in fact has deeper roots in kalam. Imagine an actually infinite regress of past causes terminating in the present effect. In this case, the regress of causes terminating, say, yesterday, or, for that matter, at any day in the infinite past, has exactly the same number of causes as the regress terminating in the present. This seems absurd, since the entire regress contains all the same causes as any selected partial regress plus an arbitrarily large number of additional causes as well. Or again, if we number the causes, there will be as many odd-numbered causes as there are causes, which seems absurd, since there are an equally infinite number of even-numbered causes in the series in addition to the self-same odd-numbered causes.

I must confess that such a situation does strike me as absurd. We can heighten the absurdity by imagining, with al-Ghazali, two beginningless series of concatenated causes. [17] He envisions our solar system existing from eternity past, the orbital periods of the planets being so co-ordinated that for every one orbit which Saturn completes Jupiter completes 2.5 times as many. If they have been orbiting from eternity, we must say that they have completed precisely the same number of orbits. But this seems absurd, for the longer they revolve the greater becomes the disparity between them, as they progressively approach a limit at which Saturn has fallen infinitely far behind Jupiter with respect to orbits completed. Yet, being now actually infinite, their respective completed orbits are somehow magically identical. Indeed, they will have “attained” infinity from eternity past: the number of completed orbits is always the same. Moreover, Ghazali asks, will the number of completed orbits be even or odd? It must be one or the other, but either answer seems absurd. We might be tempted to deny that the number of completed orbits is either even or odd. But post-Cantorian transfinite arithmetic gives a quite different answer: the number of orbits completed is both even and odd! [18] For a cardinal number n is even if there is a unique cardinal number m such that n = 2m, and n is odd if there is a unique cardinal number m such that n = 2m + 1. In the envisioned scenario the number of completed orbits is (in both cases!) ℵ0, and ℵ0 = 2ℵ0 = 2ℵ0 +1. So Jupiter and Saturn have each completed both an even and an odd number of orbits, and that number has remained equal and unchanged from all eternity, despite their ongoing revolutions and the growing disparity between them over any finite interval of time. I think Sobel would agree with me that this seems at least prima facie absurd.

Sobel observes that such scenarios bring into conflict two “seemingly innocuous” principles, namely,

and

We cannot have both of these principles along with

For Sobel the choice to be taken is clear: “The choice we have taken from Cantor is to hold on to (i) while restricting the proper submultiplicity condition to finite multiplicities. In this way we can ‘have’ comparable infinite multitudes.” [19]

But the choice taken from Cantor of which Sobel speaks is a choice on the part of the mathematical community to reject intuitionism and finitism in favor of infinite set theory. Finitism would too radically truncate mathematics to be acceptable to most mathematicians. But, as already indicated, that choice does not validate metaphysical conclusions. The metaphysician wants to know why, in order to resolve the inconsistency among (i)-(iii), it is (ii) that should be jettisoned (or restricted). Why not instead reject or restrict to finite multiplicities (i), which is a mere set-theoretical convention? More to the point, why not reject (iii) instead of the apparently innocuous (i) or (ii)? It certainly lacks the innocuousness of those principles, and giving it up would enable us to affirm both (i) and (ii). Remember: we can “have” comparable infinite multiplicities in mathematics without admitting them into our ontology. In view of the absurdities which ontologically real actual infinite multitudes would engender, perhaps we are better off without them.

Sobel thus needs some argument for the falsity of (ii). [20] It is insufficient merely to point out that if (i) and (iii) are true, then (ii) is false, for that is merely to reiterate the incompatibility of the three propositions. The opponent of (iii) may argue that if (iii) were true, then (i) would be true with respect to such a multitude, as Sobel believes; and that if (i) and (iii) were true, then the various counter-intuitive situations would result; therefore if (iii) were true, the various counter-intuitive situations would result. But because these situations are really impossible, it follows that (iii) is not possibly true. In order to refute this reasoning, one must do more than point out that if (i) and (iii) are true, then (ii) is false, for that is merely to reiterate that if an actual infinite were to exist and the correspondence principle were valid with respect to it, then the relevant situations would result, which is not in dispute.

The counter-intuitive situations which infinite multitudes legitimate can be augmented by further, more dramatic illustrations, such as Hilbert’s Hotel, a peculiar hostelry which, while having no vacancies, can always accommodate additional guests. Sobel’s retort is that the difficulties with such a hotel are practical and physical; “they bring out the physical impossibility of this particular infinity of concurrent real things, not its logical impossibility.” [21] With this response Sobel has forgotten the distinction he made earlier between “a contradiction” and “an ‘evident absurdity’.” Hilbert’s Hotel, as an illustrative embodiment of transfinite arithmetic based on axiomatic set theory will of necessity be as logically consistent as that system; otherwise it would be useless as an illustration. But it also vividly illustrates the absurd situations to which the real existence of an infinite multitude can lead. The absurdity is not merely practical and physical; it is ontologically absurd that a hotel exist which is completely full and yet can accommodate untold infinities of new guests just by moving people around.

Worse, if such a hotel could exist in reality, then it would lead to situations which would not be warranted by transfinite arithmetic and finally to logical contradictions. For while in transfinite arithmetic the inverse operations of subtraction and division of infinite quantities from or by infinite quantities is not permitted, these could occur with a real hotel occupied by real people. In such cases one winds up with logically impossible situations, such as subtracting identical quantities from identical quantities and finding non-identical differences. [22] Sobel does not even address these sorts of difficulties.

Impossibility of Forming an Infinite Multitude by Successive Addition

Quite independent of the absurdities arising from the existence of an actually infinite multitude are the further difficulties arising as a result of the temporal formation of such a multitude through a process of successive addition. Even if an actually infinite multitude of concurrent causes could exist, the idea of an actually infinite multitude of consecutive causes in a temporal series terminating in the present is notoriously difficult. One of the classic difficulties is the problem known as “the impossibility of traversing the infinite.” In order for the present event to have arrived, one would have to have successively traversed an infinite number of similar, prior events, which seems impossible.

Sobel takes Aquinas’ own answer to this objection to the infinity of the past to be sufficient: “Passage is always understood as being from term to term. Whatever by-gone day we choose, from it to the present day there is a finite number of days which can be traversed”. [23] Sobel comments,

On this analysis the traversal of an infinite series of past events is, indeed, impossible. But this impossibility arises, not because an infinite series of past events cannot be lived through, so to speak, but because the very concept of traversal involves beginning and ending points. Since in a beginningless series of past causes there is no terminus a quo, not even an infinitely distant one, one cannot say that the series of past events has been “traversed.”

This Thomistic riposte to the present objection strikes me as plainly unsatisfactory. In the first place it is not at all clear that the concept of traversal entails passing from a terminus a quo to a terminus ad quem and so the finitude of the distance traversed. To traverse a distance is to cross every proper part of it. As such traversal does not entail that the distance traversed has a beginning or ending point or a first or last part. One traverses an infinite distance if one crosses every proper part of that distance. Since, as Sobel says, every proper part of an infinite past terminating in the present is finite, no vicious circularity arises in assuming that one can cross such intervals. Second, the riposte once again trades on mere words. It is immaterial what word we use to describe the successive actualization of the series of past events; the fact is that, at least on a tensed theory of time, every proper part of the past has been lived through. The infinite multitude of past events is not simply given tenselessly but has been serially constituted through the successive addition of one element after another. [25] Third, Sobel seems to infer that because every finite part of the past can be traversed in order to arrive at this present day, therefore the whole infinite past can be traversed (or formed by successive addition). Such an inference plainly commits the fallacy of composition. Thus, the fact that any finite part of the infinite past can be traversed “one day at a time” goes no distance toward showing that the entire series can be formed by adding one day at a time.

Empirical Evidence for the Beginning of the Universe

One of the most remarkable recent developments for natural theology is that we now have powerful empirical evidence from astrophysical cosmology for the key premiss of the kalam cosmological argument. Both the evidence for the Big Bang cosmogonic theory and the evidence of the Second Law of Thermodynamics point to an absolute origin of the universe at some time in the finite past. [26] Sobel addresses the first body of evidence only, as follows:

The first thing to notice about this response is that the question it addresses--viz., if the world of sensible things began a finite time ago in the Big Bang, could there have been an infinite temporal regress of causes?--is not immediately relevant to the second premiss of the kalam cosmological argument. What we want to know is whether the evidence for the Big Bang theory supports the conclusion that the universe is finite in its past temporal duration and so began to exist, not whether an infinite series of causes can be squeezed into the metrically finite distance between the universe’s beginning and today. The Big Bang theorist can happily acquiesce in the mathematical trick of subdividing the finite past so as to form a series of prior states or “causes” converging toward the Big Bang at t = 0 as a limit. But this exercise has no direct bearing upon the question of whether the universe began to exist.

It is noteworthy that Sobel himself still speaks of “the time of the Big Bang,” which will be the time at which, according to the theory, the universe came into being. Moreover, Sobel’s concluding sentence in the above citation seems self-contradictory. The quoted conditional in the antecedent must mean that if one leaves aside the event of the Big Bang itself, then prior to any event in the convergent series of events is always another event. But then would it not also be true that in the same series there is a time correlated with every event, so that prior to any time in the series there is always an event prior to that time? The only way it could not be true that prior to any time there is an event is if one goes outside the series to consider the time t = 0 of the Big Bang itself; but then it is equally true that there is an event, namely, the Big Bang, which is prior to every other event and is absolutely first.

Sobel’s thought experiment, however, suggests to him a route of escape from the kalam cosmological argument. The fact that “There can be infinite beginningless temporal regresses of sensible-thing efficient causes . . . , even if there was a beginning . . . in the sense of a time at and before which there were no sensible things” makes trouble, he says, for the kalam argument. [28] He explains,

He sums up,

Sobel is here proposing, not only a new definition of “begins to exist,” but also a radical new cosmogony aimed at avoiding the beginning of the universe in the customary sense.

Sobel thinks that the causal principle which constitutes the first premiss of the kalamcosmological argument, namely, “Everything that begins to exist has a cause of its existence” is plausible if we understand “begins to exist” to mean “has an earliest time of its existence.” But he proposes to re-define “begins to exist” to mean “exists after some time in the past at and before which no sensible things exist.” Given this new definition, the causal principle is said to be no longer plausible but contentious. He will then claim that the evidence supports the universe’s beginning to exist in only in his re-defined sense, not in the sense of having a first time of its existence. Hence, it will remain at least contentious whether the universe requires a cause of its existence.

Whether the causal principle, once its key terms are re-defined, becomes contentious may remain moot, for Sobel’s re-definition of “begins to exist” is patently inadequate. On the re-definition it becomes analytically impossible that time began to exist or that there was a first moment of time at which the universe existed. But these are matters to be settled scientifically and metaphysically, not by definition. Stephen Hawking reports, “Almost everyone now believes that the universe, and time itself, had a beginning at the Big Bang.” [31] Sobel’s re-definition would render this consensus of contemporary cosmologists incoherent.

In any case, Sobel’s re-definition of “begins to exist” will be once again a merely verbal maneuver unless he can make it plausible that the universe did not begin to exist in the customary sense. Remember: this is supposed to be serious science, since one is appealing to the best evidence of contemporary cosmology in support of the second premiss of the kalam argument. So what is Sobel’s alternative? He proposes that prior to the origin of the universe of sensible things, there existed, like a rock out to sea, a time at and before which nothing else existed—no physical objects, since these are part of the sensible universe, no abstract objects, since these are timeless, and no God, since His existence is under dispute. There could be nothing existing at that time, lest it be the case that something began to exist in the customary sense at that time and so required an ultra-mundane cause. Some unspecified interval after this primordial time the sensible universe came into being during a half-open interval (0, 1] through a convergent series of ever more quickly (as one regresses in time) operating causes.

Scientifically, the proposed model is incoherent, since it postulates a time prior to the origin of spacetime. P. C. W. Davies points out, “Recent ideas in quantum physics have changed our picture of the origin of time somewhat, but the essential conclusion remains the same: time did not exist before the Big Bang.” [32] One cannot escape this incoherence of postulating a time before time by identifying the primordial time with the cosmological singularity itself, for not only is the singularity not an instant of time, but more importantly the entire mass-energy content of the universe and, indeed, space itself is compacted into the initial singularity, so that it is not the case that nothing exists then. The first temporal interval is in such a case a closed internal [0, 1] terminating in the singularity. Sobel’s initial time must exist, per impossibile, temporally prior to the cosmological singularity (Fig. 2) which marked the origin of time and space and beyond which the spacetime manifold cannot be extended.

Fig. 2. Sobel’s model of an initial time prior to the origin of the universe.

The only way to save Sobel’s proposal is to resort to metaphysics, to claim that the primordial time is a moment in a metaphysical time during which physical spacetime came to exist. Such a recourse would tacitly concede, however, that insofar as the scientific evidence is concerned, that evidence supports the beginning of the universe in the customary sense. Now Sobel’s metaphysical hypothesis is, I think, coherent, but what reason, other than the desire to avoid theism, is there to think that there was such a time? Do we not, on the contrary, have good reason to think that there was no such time? No relationalist could accept such a view of an initial, eventless time. Even a substantivalist like Newton would have balked at it, since Newton’s absolute time was not utterly void but was the duration of God’s being. More problematically, on a substantivalist view of time, such a moment is, in fact, a thing and its origination requires a cause. If we say that this moment was itself preceded by an infinite, empty time, then the question raised in the antithesis of Kant’s First Antinomy concerning time returns with a vengeance, for there is nothing in such a void time to distinguish one moment from another, so that why the sensible universe came into being when it did (even if lacking a first instant of its existence) becomes mysterious. Indeed, even on the supposition that a first moment of metaphysical time exists, the question still presses why the sensible universe did not come to be earlier or later than it did. Given that prior to the first half-open interval (0, 1] of the universe’s duration nothing existed apart from metaphysical time itself, the origination of the universe ex nihilo seems metaphysically absurd. Thus even given Sobel’s scenario (and how can we soberly give such a thing?), it seems plausible that the causal principle would hold for a universe which “began to exist” in Sobel’s idiosyncratic sense.

It might be suggested that we could avoid these difficulties by reverting to the definition of “begins to exist” as “has an earliest time of its existence” and then modifying Sobel’s proposed cosmogony so as to eliminate the time prior to the universe’s existence, so that the series of “fast-starting” causes converges to t=0 as a merely ideal limit. [33] On such a proposal the universe lacks a beginning point and can therefore be said to have no earliest time of its existence. Hence, it does not, despite its past temporal finitude, begin to exist, and so no cause of the universe’s origin need be postulated.

It is not clear that such a proposal is even physically possible [34] ; but let that pass. The fundamental philosophical shortcoming of this proposal is its gratuitous assumption that having a beginning entails having a beginning point. This is not, in fact, how the locution “begins to exist” is typically understood. For one thing, the proposed definition commits us to the reality of points, which surely overloads the expression “begins to exist” with unintended ontological commitments. Moreover, the use of the expression in astrophysical cosmogony belies the supposed entailment. Contemporary cosmologists frequently “cut out” the initial cosmological singularity as a merely ideal point on the boundary of spacetime so that the universe has no first instant of its existence; but they do not therefore think that the universe no longer begins to exist or that the mystery of the origin of the universe has thereby been solved.

The key idea in having a beginning is past metrical finitude. Time may be said to begin to exist just in case for any non-zero, finite interval of time that one picks, there are only a finite number of congruent intervals earlier than it. Or, alternatively, time begins to exist just in case for some specified non-zero, finite interval of time, there are no congruent intervals earlier than it. On either explication beginning to exist does not entail having a beginning point.

In affirming that the universe began to exist, the proponent of the kalam cosmological argument understands “begins to exist” in the following way, where “x” ranges over any entity and “t” ranges over times, whether instants or moments:

Ignoring nuances springing from considerations of tense and timelessness, the proponent of the cosmological argument could substitute Sobel’s principle that “everything that has a first time of its existence has a cause” for the first premiss of the kalam cosmological argument so long as by “time” one does not mean merely an instant (a degenerate temporal interval of zero duration) but any moment (a positive, finite temporal interval) as well, such as a second or hour or day.

So understood the principle seems eminently plausible. As mentioned, cosmologists continue to puzzle over the origin of the universe out of nothing whether or not it had an initial instant of its existence. One thinks in this connection of the ancient sorites-style problems of starting and stopping. [35] If there is a last instant at which some object is at rest, then when does it begin to move? The answer can only be that there is no first instant of its motion. Nonetheless, the object does begin to move and plausibly requires a cause to set it in motion. Similarly, if something begins to exist, it is plausible that it requires a cause to bring it into being whether or not there is a first instant at which it exists.

It seems to me, therefore, that neither Sobel’s attempt to avert the beginning of the universe predicted by the Big Bang theory nor the proposed modification of his view is plausible or ultimately avails in defeating the second premiss of the kalam cosmological argument.

Conclusion

Sobel reflects later in his book that “The most serious problems with first-cause arguments . . . are (i) the apparent possibility that first generating and moving causes should no longer exist and (ii) the apparent possibility . . . of infinite regresses of generating and moving causes.” [36] The first of these purportedly serious problems comes as a bit of a surprise, since Sobel devotes very little space to this consideration, which occurs as sort of afterthought to his discussion of first-cause arguments.[37] In any case, offering the decease of the cause of the universe as a mere possibility hardly seems a serious objection. I have elsewhere argued that the kalam argument issues in a personal being who transcends (physical) time and space and is the cause of all the mass-energy in the universe. [38] Hence, we might well be puzzled how any created thing could bring about his demise or how a timelessly existing being should expire of its own. At most Sobel’s concern should motivate us to seek (and hope to find) evidence of the personal Creator’s further revelation of himself in the affairs of human history.

As for the second allegedly serious problem, the mere possibility of infinite regresses of causes again would do nothing to refute the evidence of physical cosmology that no such regresses exist. Moreover, we have seen that even on Sobel’s radically revisionary cosmology, the postulation of an infinite series of causes converging toward t = 0 or beyond does nothing to alleviate the need for a cause of the origin of the universe. In any case, Sobel has not been able to show that an infinite regress of past events is possible and would not lead to situations which are, if not logically impossible, metaphysically absurd. [39]

• [1]

  Jordan Howard Sobel, Logic and Theism: Arguments for and against Beliefs in God (Cambridge: Cambridge University Press, 2004), chaps. v-vi. For his critique of the kalam cosmological argument, see pp. 181-9, 198-9, and relevant endnotes.

  Jordan Howard Sobel, Logic and Theism: Arguments for and against Beliefs in God (Cambridge: Cambridge University Press, 2004), chaps. v-vi. For his critique of the kalam cosmological argument, see pp. 181-9, 198-9, and relevant endnotes.

• [2]

  It is odd that Sobel adds the parenthetical phrase to his formulation of the argument, since it renders the argument plainly invalid. The practitioner of kalam will need to offer further argument to justify his belief that the cause of the universe is itself uncaused.

  It is odd that Sobel adds the parenthetical phrase to his formulation of the argument, since it renders the argument plainly invalid. The practitioner of kalam will need to offer further argument to justify his belief that the cause of the universe is itself uncaused.

• [3]

  Summa theologica 1.2.3.

  Summa theologica 1.2.3.

• [4]

  Sobel does not address Aquinas’ conviction that an infinite multitude of past causes would be a merely potential infinity, since all the causes do not exist in actuality.

  Sobel does not address Aquinas’ conviction that an infinite multitude of past causes would be a merely potential infinity, since all the causes do not exist in actuality.

• [5]

  Summa theologica 1.7.4.

  Summa theologica 1.7.4.

• [6]

  Sobel, Logic and Theism, 185, citing Rucker.

  Sobel, Logic and Theism, 185, citing Rucker.

• [7]

  Ibid.

  Ibid.

• [8]

  Ibid.

  Ibid.

• [9]

  On this notion see Georg Cantor, “Letter to Dedekind,” 28 July, 1899, in From Frege to Gödel: A Sourcebook in Mathematical Logic, 1879-1931, ed. Jean van Heijenoort, Sourcebooks in the History of the Sciences (Cambridge, Mass.: Harvard University Press, 1967), 114.

  On this notion see Georg Cantor, “Letter to Dedekind,” 28 July, 1899, in From Frege to Gödel: A Sourcebook in Mathematical Logic, 1879-1931, ed. Jean van Heijenoort, Sourcebooks in the History of the Sciences (Cambridge, Mass.: Harvard University Press, 1967), 114.

• [10]

  Sobel, Logic and Theism, 187.

  Sobel, Logic and Theism, 187.

• [11]

  Ibid., 29.

  Ibid., 29.

• [12]

  Ibid., 560.

  Ibid., 560.

• [13]

  Ibid., 202.

  Ibid., 202.

• [14]

  A rebutting defeater attempts to show that the disputed claim is false. An undercutting defeater aims to show that the disputed claim has not been shown to be true.

  A rebutting defeater attempts to show that the disputed claim is false. An undercutting defeater aims to show that the disputed claim has not been shown to be true.

• [15]

  Sobel, Logic and Theism, 185.

  Sobel, Logic and Theism, 185.

• [16]

  Ibid., 188-90. For another example, consider David Hume’s comment on something’s coming into being without a cause: “But allow me to tell you that I never asserted so absurd a Proposition as that anything might arise without a cause: I only maintain’d that our certainty of the Falshood of the Proposition proceeded neither from Intuition nor Demonstration; but from another source” (David Hume to John Stewart, February 1754, in The Letters of David Hume, 2 vols., ed. J. T. Grieg [Oxford: Clarendon Press, 1932], 1: 187).

  Ibid., 188-90. For another example, consider David Hume’s comment on something’s coming into being without a cause: “But allow me to tell you that I never asserted so absurd a Proposition as that anything might arise without a cause: I only maintain’d that our certainty of the Falshood of the Proposition proceeded neither from Intuition nor Demonstration; but from another source” (David Hume to John Stewart, February 1754, in The Letters of David Hume, 2 vols., ed. J. T. Grieg [Oxford: Clarendon Press, 1932], 1: 187).

• [17]

  Al-Ghazali, Tahafut al-Falasifah, trans. S. A. Kamali (Lahore: Pakistan Philosophical Congress, 1963), 20.

  Al-Ghazali, Tahafut al-Falasifah, trans. S. A. Kamali (Lahore: Pakistan Philosophical Congress, 1963), 20.

• [18]

  See Waclaw Sierpinski, Cardinal and Ordinal Numbers, Polska Akademia Nauk Monografie Matematyczne 34 (Warsaw: Panstwowe Wydawnictwo Naukowe, 1958), 146.

  See Waclaw Sierpinski, Cardinal and Ordinal Numbers, Polska Akademia Nauk Monografie Matematyczne 34 (Warsaw: Panstwowe Wydawnictwo Naukowe, 1958), 146.

• [19]

  Sobel, Logic and Theism, 186-7.

  Sobel, Logic and Theism, 186-7.

• [20]

  Sobel does claim that Aquinas could have been persuaded to give up (i) or (ii), since he believed in the reality of the natural numbers and so could have felt compelled to admit that there is an infinite multitude of them. But that fails to reckon with Thomas’s view on the nature of abstract objects. Aquinas like other medievals embraced the Augustinian view that Platonic objects were, in fact, not mind-independent realities but rather the divine ideas. Moreover, since Aquinas held God’s cognitive state to be absolutely simple, He does not really have a multiplicity of ideas. Rather the plurality of divine ideas is the representation we finite knowers are constrained to make of Gods’ simple intuition of all truth. The implication would seem to be that numbers have only a conceptual reality as they are cognized by finite knowers. Thus, we have in Aquinas a sort of intuitionistic constructivist view of mathematical objects.

  Sobel does claim that Aquinas could have been persuaded to give up (i) or (ii), since he believed in the reality of the natural numbers and so could have felt compelled to admit that there is an infinite multitude of them. But that fails to reckon with Thomas’s view on the nature of abstract objects. Aquinas like other medievals embraced the Augustinian view that Platonic objects were, in fact, not mind-independent realities but rather the divine ideas. Moreover, since Aquinas held God’s cognitive state to be absolutely simple, He does not really have a multiplicity of ideas. Rather the plurality of divine ideas is the representation we finite knowers are constrained to make of Gods’ simple intuition of all truth. The implication would seem to be that numbers have only a conceptual reality as they are cognized by finite knowers. Thus, we have in Aquinas a sort of intuitionistic constructivist view of mathematical objects.

• [21]

  Sobel, Logic and Theism, 187.

  Sobel, Logic and Theism, 187.

• [22]

  It will not do, in order to avoid the contradiction, to assert with an anonymous referee that there is nothing in transfinite arithmetic that forbids using set difference to form sets. Indeed, the thought experiment assumes that we can do such a thing. Removing all the guests in the odd-numbered rooms always leaves an infinite number of guests remaining, and removing all the guests in rooms numbered greater than four always leaves four guests remaining. That does not change the fact that in such cases identical quantities minus identical quantities yields non-identical quantities, a contradiction.

  It will not do, in order to avoid the contradiction, to assert with an anonymous referee that there is nothing in transfinite arithmetic that forbids using set difference to form sets. Indeed, the thought experiment assumes that we can do such a thing. Removing all the guests in the odd-numbered rooms always leaves an infinite number of guests remaining, and removing all the guests in rooms numbered greater than four always leaves four guests remaining. That does not change the fact that in such cases identical quantities minus identical quantities yields non-identical quantities, a contradiction.

• [23]

  Summa theologica 1.46.2.

  Summa theologica 1.46.2.

• [24]

  Sobel, Logic and Theism, 182.

  Sobel, Logic and Theism, 182.

• [25]

  In this and other ways the kalam cosmological argument is intimately bound up with a tensed theory of time. For discussion see my The Tensed Theory of Time: A Critical Examination, Synthese Library 293 (Dordrecht: Kluwer Academic Publishers, 2000); The Tenseless Theory of Time: A Critical Examination, Synthese Library 294 (Dordrecht: Kluwer Academic Publishers, 2000).

  In this and other ways the kalam cosmological argument is intimately bound up with a tensed theory of time. For discussion see my The Tensed Theory of Time: A Critical Examination, Synthese Library 293 (Dordrecht: Kluwer Academic Publishers, 2000); The Tenseless Theory of Time: A Critical Examination, Synthese Library 294 (Dordrecht: Kluwer Academic Publishers, 2000).

• [26]

  For a review see my “Naturalism and Cosmology,” in Analytic Philosophy without Naturalism, ed. A. Corradini, S. Galvan, and J. Lowe (London: Routledge, 2005) and my “Time, Eternity, and Eschatology,” in Oxford Handbook on Eschatology, ed. J. Walls (Oxford: Oxford University Press, forthcoming).

  For a review see my “Naturalism and Cosmology,” in Analytic Philosophy without Naturalism, ed. A. Corradini, S. Galvan, and J. Lowe (London: Routledge, 2005) and my “Time, Eternity, and Eschatology,” in Oxford Handbook on Eschatology, ed. J. Walls (Oxford: Oxford University Press, forthcoming).

• [27]

  Sobel, Logic and Theism, 198.

  Sobel, Logic and Theism, 198.

• [28]

  Ibid.

  Ibid.

• [29]

  Ibid.

  Ibid.

• [30]

  Ibid., 198-9.

  Ibid., 198-9.

• [31]

  Stephen Hawking and Roger Penrose, The Nature of Space and Time, The Isaac Newton Institute Series of Lectures (Princeton, N. J.: Princeton University Press, 1996), 20.

  Stephen Hawking and Roger Penrose, The Nature of Space and Time, The Isaac Newton Institute Series of Lectures (Princeton, N. J.: Princeton University Press, 1996), 20.

• [32]

  Paul Davies, About Time (New York: Simon & Schuster, 1995), 132.

  Paul Davies, About Time (New York: Simon & Schuster, 1995), 132.

• [33]

  I owe this suggestion to an anonymous referee. I encountered a similar suggestion from Quentin Smith on the occasion of the forum “Science and Religion,” University of California, Santa Barbara, January 30, 2004, featuring William Lane Craig, Richard Gale, Alvin Plantinga, and Quentin Smith, available in DVD format through http://www.veritas-ucsb.org/. See also Adolf Grünbaum, “A New Critique of Theological Interpretations of Physical Cosmology,” British Journal for the Philosophy of Science 51 (2000): 16-17.

  I owe this suggestion to an anonymous referee. I encountered a similar suggestion from Quentin Smith on the occasion of the forum “Science and Religion,” University of California, Santa Barbara, January 30, 2004, featuring William Lane Craig, Richard Gale, Alvin Plantinga, and Quentin Smith, available in DVD format through http://www.veritas-ucsb.org/. See also Adolf Grünbaum, “A New Critique of Theological Interpretations of Physical Cosmology,” British Journal for the Philosophy of Science 51 (2000): 16-17.

• [34]

  It will depend crucially on one’s theory of quantum gravity. A typical approach to marrying quantum theory to General Relativity involves describing the evolution of spacetime as a path integral (a sum over all possible paths) in superspace, which is a space of points respresenting three-dimensional configurations of the universe. The points of this configuration space can be regarded as instantaneous states or even as instants, but the fact that in the quantum theory one has a path integral, rather than a single path, makes it impossible to “stack” these instants into a unique history constituting a spacetime. So eventually the dividing process envisioned by Sobel becomes ill-defined in the theory. The fact that the first split-second of the universe’s existence as measured in cosmic time is not resolvable into a unique sequence of ever briefer states is not inconsistent with there being a first second of its existence. I am grateful to Donald Page for an accurate articulation of this concern.

  It will depend crucially on one’s theory of quantum gravity. A typical approach to marrying quantum theory to General Relativity involves describing the evolution of spacetime as a path integral (a sum over all possible paths) in superspace, which is a space of points respresenting three-dimensional configurations of the universe. The points of this configuration space can be regarded as instantaneous states or even as instants, but the fact that in the quantum theory one has a path integral, rather than a single path, makes it impossible to “stack” these instants into a unique history constituting a spacetime. So eventually the dividing process envisioned by Sobel becomes ill-defined in the theory. The fact that the first split-second of the universe’s existence as measured in cosmic time is not resolvable into a unique sequence of ever briefer states is not inconsistent with there being a first second of its existence. I am grateful to Donald Page for an accurate articulation of this concern.

• [35]

  See Richard Sorabji, Time, Creation, and the Continuum (Ithaca, N.Y.: Cornell University Press, 1983), 403-21.

  See Richard Sorabji, Time, Creation, and the Continuum (Ithaca, N.Y.: Cornell University Press, 1983), 403-21.

• [36]

  Sobel, Logic and Theism, 200.

  Sobel, Logic and Theism, 200.

• [37]

  Ibid., 193-4.

  Ibid., 193-4.

• [38]

  On the personhood and other attributes of the transcendent cause of the beginning of the universe see my and Paul Copan’s Creation out of Nothing (Grand Rapids, Mich.: Baker, 2004), 252-4.

  On the personhood and other attributes of the transcendent cause of the beginning of the universe see my and Paul Copan’s Creation out of Nothing (Grand Rapids, Mich.: Baker, 2004), 252-4.

• [39]

  My thanks to J. Howard Sobel for his kind responses to my interpretive questions concerning his text. Thanks are due as well to an anonymous referee for his constructive criticisms.

  My thanks to J. Howard Sobel for his kind responses to my interpretive questions concerning his text. Thanks are due as well to an anonymous referee for his constructive criticisms.