


God and the Platonic Host
William Lane CraigSummary
This paper, presented before the C. S. Lewis Society in Oxford on the fiftieth anniversary of his death, surveys the options available to the theist for meeting the challenge posed by platonism to divine aseity and shows that Lewis anticipated a figuralist solution to the problem.
Central to classical theism is the conception of God as the sole ultimate reality, the Creator of all things apart from Himself. This doctrine receives its most significant challenge from Platonism, the view that there are uncreated abstract objects, such as numbers, sets, propositions, and so forth. According to Platonism there is a host of objects, indeed, infinities of infinities of beings, which are just as eternal, necessary, and uncreated as God. So God is not the sole ultimate reality.
I should perhaps clarify that I speak here, not of what is been called “lightweight” Platonism, but of a “heavyweight” Platonism. Lightweight Platonism treats abstract objects merely as the semantic referents of certain singular terms like proper names and definite descriptions. On lightweight Platonism abstract objects are individuals merely in the sense that Wednesdays and the hole in your shirt are individuals, namely, as referents of the terms “Wednesday” and “the hole in your shirt,” but not in a sense which would require God to create such things in order for us to speak meaningfully of their existence. I am talking about “heavyweight” Platonism, according to which abstract objects exist just as robustly as the fundamental particles which make up the physical world. Such a Platonism saddles us with a metaphysical pluralism according to which God is not the sole ultimate reality. Rather there are infinite realms of beings which exist independently of God. How is this challenge best to met?
Theological Prolegomena
It is not to be met, I believe, by theological compromise. For the biblical witness to God’s sole ultimacy is both abundant and clear. Undoubtedly one of the most important biblical texts, both theologically and historically, in this regard is the third verse of the prologue of the Gospel of John. Speaking of the pre-incarnate Christ as the Logos or Word (1.14), John [1] writes,
In the beginning was the Word,
and the Word was with God,
and the Word was God.
He was in the beginning with God.
All things came into being through him,
and without him not one thing came into being. (1.1-3).
“All things” (πάντα) connotes all things taken severally, not simply the Whole. Of course, God is implicitly exempted from inclusion in “all things,” since He has already been said to have been (ἦν) in the beginning (ἐν ἀρχῇ) (v. 1). God and the Logos are not the subject of becoming or coming into being, but of being simpliciter. They simply were in the beginning. Everything other than God and the divine Logos “came into being” (ἐγένετο) through the Logos. The verb is the aorist form of γίνομαι, whose primary meaning is “to become” or “to originate.” V. 3 thus carries the weighty metaphysical implication that there are no eternal entities apart from God. Rather everything that exists, with the exception of God Himself, is the product of temporal becoming. [2]
The verb γίνομαι also has the sense of “to be created” or “to be made.” This meaning emerges in v. 3 through the denomination of the agent (δι’ αὐτοῦ) responsible for things’ coming into being. The preposition δία + genitive indicates the agency by means of which a result is produced. The Logos, then, is said to be the one who has created all things and brought them into being. A second, equally significant metaphysical implication of v. 3 thus emerges: only God is self-existent; everything else exists through another, namely, through the divine Logos. God is thus the ground of being of everything else.
Jn. 1.3 is thus fraught with metaphysical significance, for taken prima facie it tells us that God alone exists eternally and a se. It entails that there are no objects of any sort, abstract or concrete, which are co-eternal with God and uncreated by God via the Logos.
Partisans of uncreated abstract objects, if they are to be biblical, must therefore maintain that the domain of John’s quantifiers is restricted in some way, quantifying, for example, only over concrete objects. The issue is a subtle one, easily misunderstood. [3] The question is not: did John have in mind abstract objects when he wrote πάντα δι’ αὐτοῦ ἐγένετο? Probably not. But neither did he have in mind quarks, galaxies, and black holes; yet he would take such things and countless other things, were he informed about them, to lie within the domain of his quantifiers. The question is not what John thought lay in the domain of his quantifiers. The question, rather, is: did John intend the domain of his quantifiers to be unrestricted, once God is exempted? It is very likely that he did. For not only is God’s unique status as the only eternal, uncreated being typical for Judaism, but John himself identifies the Logos alone as existing with God (and being God) in the beginning. Creation of everything else through the Logos then follows. The salient point here is that the unrestrictedness of the domain of the quantifiers is rooted, not in the type of objects thought to be in the domain, but in one’s doctrine of God as the only uncreated being.
But was John, in fact, ignorant of the relation between abstract objects and divine creation when he wrote vv. 1-3, as we have assumed? It is, in fact, far from clear that the author of John’s prologue was innocent concerning abstract objects and their relation to the Logos. For the doctrine of the divine, creative Logos was widespread in Middle Platonism, [4] and the similarities between John’s Logos doctrine and that of the Alexandrian Jewish philosopher Philo (20 B.C.-A.D. 50) are numerous and striking. [5] Of particular interest is the role of the Logos as the instrumental cause of creation. The use of δια + genitive to express instrumental creation is not derived from Wisdom literature but is an earmark of Middle Platonism; indeed, so much so that scholars of this movement are wont to speak of its “prepositional metaphysics,” whereby various prepositional phrases are employed to express causal categories: [6]

Philo identifies the four Aristotelian causes by these prepositional phrases, stating that the phrase “through which” represents creation by the Logos. [7]
The similarities between Philo and John’s doctrines of the Logos are so numerous and close that most Johannine scholars, while not willing to affirm John’s direct dependence on Philo, do recognize that the author of the prologue of John’s Gospel shares with Philo a common intellectual tradition of Platonizing interpretation of Genesis chapter one.
Now John does not tarry to reflect on the role of the divine Logos causally prior to creation. But this pre-creation role features prominently in Philo’s Logos doctrine. According to Philo scholar David Runia, a cornerstone of Middle Platonism was the bifurcation of the intelligible and sensible realms. [8] To draw the distinction in this way is, however, somewhat misleading. [9]The fundamental distinction here, as originally found in Plato, is between the realm of static being (τί τὸ ὄν ἀεί) and the realm of temporal becoming (τί τὸ γιγνόμενον μὲν ἀεί). The former realm is to be grasped by the intellect, whereas the latter is perceived by the senses. The realm of becoming was comprised primarily of physical objects, while the static realm of being was comprised of what we would today call abstract objects. For Middle Platonists, as for Plato, the intelligible world (κόσμος νοητός) served as a model for the creation of the sensible world. But for a Jewish monotheist like Philo, the realm of Ideas does not exist independently of God but as the contents of His mind. The intelligible world may be thought of as either the causal product of the divine mind or simply as the divine mind itself actively engaged in thought. Especially noteworthy is Philo’s insistence that the world of Ideas cannot exist anywhere but in the divine Logos. Just as the ideal architectural plan of a city exists only in the mind of the architect, Philo explains, so the ideal world exists solely in the mind of God.
On Philo’s doctrine, then, there is no realm of independently existing abstract objects. According to Runia, while not part of the created realm, “the κόσμος νοητός, though eternal and unchanging, must be considered dependent for its existence on God.” [10]
Interested as John is in the incarnation of the Logos, he does not linger over the pre-creatorial function of the Logos, but given the provenance of the Logos doctrine, he may well have been aware of the role of the Logos in grounding the intelligible realm as well as his role in creating the realm of temporal concrete objects.
However this may be, our exegetical study of Jn 1.1-3 leads to the conclusion that the author of the prologue of John’s Gospel conceives of God as the creator of everything apart from Himself. There are no uncreated, independently existing, eternal objects, for God exists uniquely a se.
I could make exactly the same point from Paul’s correspondence, but time compels me to skip ahead.
The conviction that God is the Creator of everything that exists aside from God Himself eventually attained credal status at the Council of Nicaea. In language redolent of the prologue to the fourth Gospel and of Paul, the Council affirmed:
I believe in one God, the Father, Almighty, Maker of heaven and earth and of all things visible and invisible;
And in one Lord, Jesus Christ, the only Son of God, begotten of the Father before all ages, light from light, true God from true God, begotten not made, consubstantial with the Father, through whom all things came into being.
The phrase “Maker of heaven and earth and of all things visible and invisible” is Pauline, and the expression “through whom all things came into being” Johannine. The Council thus confesses that God alone is uncreated and that all else was created by Him.
The Challenge of Platonism
The biblical theist cannot therefore be a Platonist, for Platonism denies that God is the sole ultimate reality. So how shall the classical theist best meet the challenge of Platonism? Figure 1 lays out some of the alternatives.
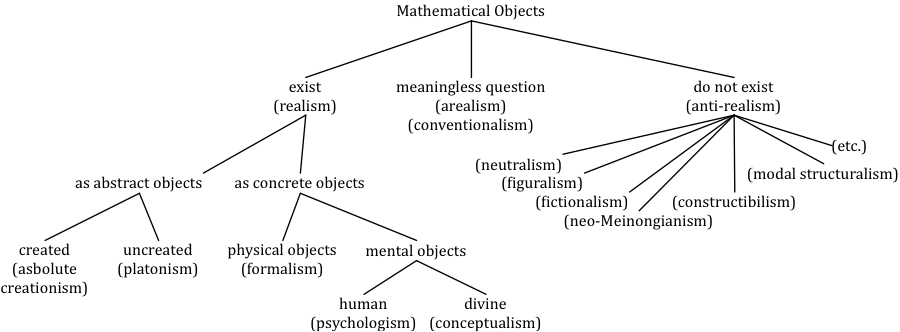
Fig. 1: Some options concerning the existence of mathematical objects.
I have taken mathematical objects as representative of what are typically taken to be abstract objects. One cannot take Fig. 1 to be about abstract objects as such because, as you can see, one branch of realism treats these objects as concrete, not abstract. Note that what I have called anti-realism often goes under the name of nominalism; but I have avoided that label as less clear and potentially misleading.
Arealism
So consider our options. I take it that a classical theist cannot embrace arealism as his solution. As I use the term, arealism is the view that there just is no fact of the matter concerning the existence of putative abstract objects. [11] Arealism is not an option for the classical theist, since, given divine aseity, God exists in every possible world and is the creator of any reality extra se in any world in which He exists. Therefore, it is a metaphysically necessary truth that no uncreated, abstract objects exist. Hence, there is, indeed, a fact of the matter whether uncreated abstract objects exist: they do not and cannot exist. Thus, arealism with respect to putative abstract objects is necessarily false.
Realism
So now consider the realist options. The option requiring the least modification of Platonism is absolute creationism. Although there is a tendency to conflate absolute creationism with divine conceptualism, I take the absolute creationist to affirm that mathematical objects are not concrete objects, like mental events, but are causally effete objects existing in some sense apart from God, though causally dependent upon Him. [12] Unfortunately, absolute creationism appears to involve a vicious circularity which has become known as the bootstrapping objection. The problem can be simply stated with respect to the creation of properties, a paradigmatic case of abstract objects. In order to create properties, God must already possess properties. For example, in order to create the property being powerful God must already possess the property of being powerful, which involves a vicious circularity. The only plausible way to avoid the bootstrapping problem, it seems to me, is to affirm that God can create a property without having the property of being able to create a property. But that just is to abandon platonism in favor of nominalism, which holds that talk of properties is just a convenient façon de parler. Such a solution removes any motivation for realism.
So what about anti-platonist forms of realism? Anti-platonist realists hold that various objects normally thought to be abstract, such as mathematical objects, are in fact concrete. These may be taken to be either physical objects, such as marks on paper which are manipulated by mathematicians according to certain rules, or mental objects or thoughts, either in human minds or in God’s mind. The 19th century German philosopher Gottlob Frege subjected the views that mathematical objects are physical objects or human thoughts to such withering criticism that such views are scarcely taken seriously today. [13] But Frege’s objections to human psychologism—such as the intersubjectivity, necessity, and plenitude of mathematical objects—do not touch divine conceptualism. That Frege could simply overlook what has historically been the mainstream theistic position with respect to putative abstract objects is perhaps testimony to how utterly detached 19th century philosophical thinking had become from the historic Christian tradition. With the late 20th century renaissance of Christian philosophy, divine conceptualism is once more finding articulate defenders. [14] According to these thinkers putative abstract objects like propositions, properties, possible worlds, and mathematical objects are, or are analyzable in terms of, God’s thoughts of various sorts.
Conceptualists can meet the bootstrapping objection by denying that prior to God’s conceiving them things like properties, propositions, and the like exist. God can be as He is without exemplifying properties or propositions’ being true logically prior to His conceiving them. But then, as noted before, the nerve of realism seems to be cut. So why not be an anti-realist?
Moreover, conceptualism is not entirely worry-free. For in many cases God’s thoughts do not seem suitable to play the roles normally ascribed to abstracta. Take propositions, for example. Conceptualism requires that God be constantly entertaining actual thoughts corresponding to every proposition. But conceptualists move far too hastily from the fact that God is omniscient to the view that all that God knows is occurrent in consciousness. God’s infinite knowledge is clearly not sufficient to guarantee that there are the actual mental events needed by the conceptualist. Indeed, Graham Oppy complains that conceptualism “threatens to lead to the attribution to God of inappropriate thoughts: bawdy thoughts, banal thoughts, malicious thoughts, silly thoughts, and so forth.” [15] For example, consider propositions of the form for any real number r, r is distinct from the Taj Mahal. Why would God retain such inanities constantly in consciousness? Worse, consider false propositions of the form for any real number r, r is identical to the Taj Mahal. Why would God hold such a silly thought constantly in consciousness, knowing it to be false? Obviously, the concern is not that God would be incapable of keeping such a non-denumerable infinity of thoughts ever in consciousness, but rather why He would dwell on such trivialities.
Furthermore, what has been called the “aspectual shape” of a thought does not always correspond to the aspectual shape of the proposition expressed. For example, the thought that I am making a mess has a different aspectual shape than the proposition William Craig is making a mess. God can know the propositional content of my thought without His thought’s having the same aspectual shape as my thought. But if we identify God’s thoughts with propositions, we are no longer able to distinguish between the aspectual shape of a proposition and the aspectual shape of a divine thought having that propositional content. Since God has first-person thoughts, identifying God’s thoughts with propositions commits us to the existence of purely private propositions which are incommunicable by God to us. Personal indexical beliefs are just the proverbial camel’s nose. If propositions have the unique aspectual shape of God’s thoughts, many other dislocations in how we normally conceive things will be forced upon us.
In these and many other ways, the suitability of God’s thoughts to play successfully the roles ascribed to various abstracta is worrisome.
Anti-Realism
Now I do not imagine that these worries constitute insuperable obstacles for conceptualism. Rather my reason for raising them is to motivate theists to look more seriously at the cornucopia of anti-realist options that are available today. It is striking how little cognizance contemporary theists who have written on the problematic of divine aseity take of anti-realism. They seem to have absorbed realism with their mother’s milk.
It is not as though there are overwhelming arguments for realism. The principal argument offered on behalf of realism comes in the various incarnations of Willard Quine’s Indispensability Argument. Mark Balaguer succinctly formulates the Indispensability Argument as follows:
(I) If a simple sentence (i.e., a sentence of the form ‘a is F’) is literally true, then the objects that its singular terms denote exist. (Likewise, if an existential sentence (e.g., ‘There is an F’) is literally true, then there exist objects of the relevant kinds.
(II) There are literally true simple sentences containing singular terms that refer to things that could only be abstract objects. (Likewise, there are literally true existential statements whose existential quantifiers range over things that could only be abstract objects.)
(III) Therefore, abstract objects exist.
How might we respond to this argument? Although, to my knowledge, C. S. Lewis did not interact with the Indispensability Argument for abstract objects, I think we have some idea of how he might have responded to it. In his essay “Bluspels and Flalansferes: A Semantic Nightmare,” Lewis claims that the greater part of our language is metaphorical rather than literal. Lewis argues that, “Our thought is independent of the metaphors we employ in so far as these metaphors are optional: that is, in so far as we are able to have the same idea without them.” [16] Lewis uses the example of trying to understand unimaginable higher-dimensional realities like curved 3-dimensional space on the basis of 2-dimensional analogies in Flatland. In so far as one understands the relevant mathematics, one may dispense with the metaphor. But then Lewis proceeds to say,
Our claim to independence of the metaphor is . . . a claim to know the object otherwise than through that metaphor. . . . That was what happened, you will remember, to the man who went on and learned mathematics. He came to apprehend that of which the Flatlanders’ sphere was only the image, and consequently was free to think beyond the metaphor and to forget the metaphor altogether. In our previous account of him, however, we carefully omitted to draw attention to one very remarkable fact: namely, that when he deserted metaphor for mathematics, he did not really pass from symbol to symbolized, but only from one set of symbols to another. The equations and what-nots are as unreal, as metaphorical, if you like, as the Flatlanders’ sphere. [17]
It is evident that Lewis is an anti-realist about mathematical discourse, taking it to be metaphorical and its objects unreal. Lewis thinks that in many fields of discourse the failure to realize that one is using dead metaphors with no understanding of their meaning leads to the meaninglessness of that discourse. He is more optimistic with respect to mathematical discourse: “the mathematician, who seldom forgets that his symbols are symbolic, may often rise for short stretches to ninety per cent. of meaning and ten of verbiage.” [18] Lewis thus thinks that mathematicians themselves realize that their discourse is not literal but metaphorical.
Lewis was apparently also an anti-realist about other abstract objects. For example, with respect to universals, he opined, “the universal latent in every group and every plural inflection cannot be thought without metaphor.” [19] Indeed, it is likely that he took the whole platonic host to be creatures of metaphor, for he writes, “open your Plato, and you will find yourself among the great creators of metaphor, and therefore among the masters of meaning.” [20]
I think that Lewis would therefore challenge premiss (II) of the Indispensability Argument. He would contend that abstract object discourse is plausibly taken to be metaphorical, not literal, and therefore is non-commissive ontologically to abstract objects.
What shall we make of this response? The claim that abstract object discourse in general, and mathematical discourse in particular, is metaphorical rather than literal is championed today by Stephen Yablo, who has coined the term “figuralism” for the view that such discourse should not be understood literally but is a case of figurative language. Figurative speech, properly interpreted, may be true even if, taken literally, it is false. For in figurative speech, such as understatement, hyperbole, and metaphor, the literal content is not what the speaker is asserting. [21] If mathematical language is figurative, then it will be maladroit to ask after the ontological commitments of such discourse when construed literally.
Yablo observes that figurative language is a pervasive feature of ordinary discourse, so much so that we often do not realize that we are speaking figuratively. Like Lewis, Yablo believes that literal talk is actually the talk that is unusual. [22] This presents a serious problem for Quine’s project of determining the ontological commitments of our discourse. Since figures of speech should not be taken literally, Quine recognized that his criterion of ontological commitment could not be applied to such discourse. This situation is problematic because, in Yablo’s words, “To determine our ontological commitments, we have to ferret out all traces of non-literality in our assertions; if there is no sensible project of doing that, there is no sensible project of Quinean ontology.” [23]
Quine looked to science in order to eliminate metaphorical features of ordinary discourse: we are to count a thing as existing just in case it is a commitment of our best scientific theory. But, Yablo demands, what if our best theory itself contains metaphorical elements? Quine never argued that metaphor can be made to disappear entirely. If our best theories include metaphorical sentences, then we need a way of sequestering the metaphors. But in order to do that, we need a criterion for identifying an expression as metaphorical, which we do not have. The boundaries of the literal, Yablo maintains, are so unclear that there is no telling, in cases of interest, whether our assertions are to be taken ontologically seriously. The more controversial of philosophical existence claims are equipoised between the literal and the figurative in a way that Quine’s method is powerless to address. [24] Among these will be claims about abstract objects.
Yablo thinks that talk of abstract objects involves the use of what he calls “existential metaphors,” that is to say, metaphors “making play with a special sort of object to which the speaker is not [ontologically] committed.” [25] Numerical terms are such existential metaphors, useful, and sometimes indispensable, for expressing truths about the real world. Yablo provides the following illustration:
Much as we make as if, e.g., people have associated with them stores of something called ‘luck,’ so as to be able to describe some of them metaphorically as individuals whose luck is ‘running out,’ we make as if pluralities have associated with them things called ‘numbers,’ so as to be able to express an (otherwise hard to express because) infinitely disjunctive fact about relative cardinalities like so: The number of Fs is divisible by the number of Gs. [26]
Given our finitude, we cannot express infinite disjunctions like “There is one star and one planet, or there are two stars and one planet, or . . .” and so have no choice but to resort to number talk in order to talk, in this case, about stars and planets. “It is only by making as if to countenance numbers, that one can give expression in English to a fact having nothing to do with numbers, a fact about stars and planets and how they are numerically proportioned.” [27]
Yablo draws a number of very interesting parallels between talk of platonic objects [28] and figurative talk. These parallels serve as evidence that abstract object talk is a kind of figurative language. [29]
Yablo thinks that the decision between platonism and figuralism depends upon the answers to the following questions: (1) what does platonism/figuralism help us to explain, and (2) what explanatory puzzles does platonism/figuralism generate?
Consider first question (2). Yablo believes that anti-platonists have relied too heavily on the explanatory puzzles generated by platonism, though he takes no cognizance of the theological puzzle that drives our inquiry, namely, how the putative existence of abstract objects is to be reconciled with divine aseity and creatio ex nihilo. Given our theological commitments, we know that platonism is unacceptable. So all we need from Yablo, then, is some reason to prefer figuralism above other anti-platonisms. Yablo has done a good job of laying out the case for taking abstract object discourse as figurative, but he does not examine the comparative explanatory power of other anti-platonistic views with respect to the data. So more work needs to be done.
As for explanatory puzzles generated by figuralism, Yablo considers only the objection that abstract object talk, and particularly mathematical discourse, is not plausibly a matter of make-believe. This objection, however, is really an objection to a pretense theoretical analysis of figurative language, not to the figuralist thesis that abstract object talk is figurative. Consideration of such a puzzle is therefore better reserved for another time when discussing pretense theory.
So let us consider instead an objection that has been raised against Figuralism by John Burgess and Gideon Rosen. They think that the claim that mathematical discourse is figurative is implausible. They write,
Certainly in all clear cases of figurative language—and it is worth stressing that the boundary between figurative and literal is as fuzzy as can be—the non-literal character of the linguistic performance will be perfectly obvious as soon as the speaker is forced to turn attention to the question of whether the remark was meant literally.
We further submit that mathematical discourse fails this test for non-literalness. [30]
One is tempted to ask what evidence can be cited in support of their opening sentence, but never mind. The more important point is that this objection, if sound, at best proves that mathematical discourse is not a clear case of figurative language, a hardly surprising result. [31] What does not follow is that mathematical discourse does not lie somewhere in that fuzzy area between clearly figurative and clearly literal expressions.
The second and perhaps more important point to make is that while Yablo, like Lewis, espouses Figuralism as a hermeneutic thesis about how mathematicians themselves understand their discourse, there is no reason the anti-realist has to present it as such. In the absence of linguistic and sociological studies about what the community of working mathematicians think about this question, the figuralist can remain agnostic about hermeneutical questions and present the figurative interpretation simply as one reasonable way of understanding abstract object talk. If such an interpretation is reasonable, then the Indispensability Argument has been defeated.
Turn now to question (1). What are the alleged explanatory benefits of platonism? The principal merit claimed on behalf of platonism is that it provides a basis for the objective truth of mathematics. [32] But here the difference between fictionalism and figuralism comes clearly to the fore. Figuralism affirms the truth of mathematical sentences, for these are figurative speech and as such escape the traditional criterion of ontological commitment. Just as “It’s raining cats and dogs!” may be true without there being animals falling from the sky, so the truth that “1+1=2” does not require the reality of numbers. Of course, the theistic figuralist who does not believe in abstract objects will deny the literal truth of figurative talk about abstract objects; but he will insist on the truth of such statements when understood, not literally, but figuratively.
Still we may wonder what the objective basis of mathematical truths is, if not the reality of the objects referred to or quantified over in such statements. Here Yablo seems to differ from Lewis, who seemed to think that we could explain mathematical metaphors only in terms of more metaphors. Yablo maintains that the real content of mathematical truths is logical truths, which require no ontological foundation: “Arithmetic is, at the level of real content, a body of logical truths—specifically, logical truths about cardinality—while set theory consists at the level of real content, of logical truths of a combinatorial nature.” [33] In short, the realist has no advantage over the anti-realist in accounting for the objectivity of mathematical truth, since the real content of metaphorical statements about such imaginary entities as numbers and sets is logical truths.
Finally, as for the explanatory benefits of figuralism, although Yablo has benefits of his own in mind, surely for the theist the most important benefit is that it explains how to reconcile mathematical truth with divine aseity. The theist has good reasons for thinking that platonism is false and may embrace figuralism’s account of mathematics’ necessity, apriority, and absoluteness without compromising his anti-realism about abstracta.
In sum, it seems to me that figuralism is a plausible option for the theist to pursue as a means of defeating the Indispensability Argument for platonism. It offers an interpretation of abstract object discourse which is figurative, not literal, thereby avoiding ontological commitment while preserving truth. Figuralism has the additional advantage of being a very plausible interpretation of mathematical discourse in view of the striking similarities of such discourse to figurative speech.
Figuralism thus offers an attractive solution to the challenge of platonism to God’s being the sole ultimate reality. What figuralism does leave unchallenged, though, is the Quinean metaontological criterion for ontological commitment which comes to expression in premiss (I) of the Indispensability Argument. Some might see this as an advantage of figuralism, since it places figuralism on common ground concerning customary views of quantification and reference. Other anti-realists, however, will see this strategy as timid and insufficiently radical. These other anti-realists will dare to assail the sanctuary of Quinean metaontology itself.
In his earlier work, Yablo contrasted the literal and metaphorical content of a figurative sentence (“Does Ontology Rest on a Mistake?,” pp. 248-9), but was not always consistent with his later use of terminology. For example, the existentially metaphorical statement “The average star has 2.4 planets” can be paraphrased as “The number of planets divided by the number of stars is 2.4.” This eliminates the average star, but only at the expense of committing us to numbers. Since numbers are not the cosmologist’s concern, says Yablo, this statement is also metaphorical. Yablo would later put it differently: numbers are therefore platonic. Therefore, the figuralist will take the paraphrase to be metaphorical. Yablo then says that the more literal content is “There are 12 planets and 5 stars or there are 24 planets and 10 stars or . . . .” But later Yablo would realize that such a statement actually gives, not the literal content, but the real content, and does not commit its user to numbers. Because the real content is inexpressible, being an infinite disjunction, we have no recourse but to resort to metaphor, such as those used in the original statement and its paraphrase.
In his later work, Yablo tends to contrast the literal content of figurative speech with its real content (“Go Figure,” pp. 94-5; idem, “Abstract Objects,” pp. 209-30). There he explains that for the figuralist “The average mother has 2.3 children, but there is no average mother” is true because the first clause is figurative and the second literal. The real content of the first clause will be an inexpressible, infinite disjunction.
-
[1]
I use the name of the received author of the fourth Gospel without commitment to its actual authorship or to the evangelist’s authorship of the prologue. Many Johannine commentators think that the prologue contains an independent poem or hymn, perhaps stemming from the Johannine community, which has been adopted by the evangelist and supplemented with his explanatory glosses. There is unanimity that vv. 1-5 ( with possible exception of v.2), 10-11, and 14 belong to the original poem or hymn; vv. 6-9 are clearly the evangelsist’s gloss. Our interest is solely in what vv. 1-3 of the prologue mean.
I use the name of the received author of the fourth Gospel without commitment to its actual authorship or to the evangelist’s authorship of the prologue. Many Johannine commentators think that the prologue contains an independent poem or hymn, perhaps stemming from the Johannine community, which has been adopted by the evangelist and supplemented with his explanatory glosses. There is unanimity that vv. 1-5 ( with possible exception of v.2), 10-11, and 14 belong to the original poem or hymn; vv. 6-9 are clearly the evangelsist’s gloss. Our interest is solely in what vv. 1-3 of the prologue mean.
-
[2]
This implication reinforces the point which we have elsewhere made that the biblical concept of creation is an inherently temporal notion (Paul Copan and William Lane Craig, Creation out of Nothing: A Biblical, Philosophical, and Scientific Exploration [Grand Rapids, Mich.: Baker Bookhouse, 2004], chaps. 1-4). N.B. that to say that everything other than God has a temporal beginning is not to say that there is a temporal beginning of all things collectively. Theoretically, the sequence of past events could be enumerated by the negative numbers, beginning with the present event as 0, so that while everything that exists has individually a moment of its creation at some time in the finite past, nevertheless the series of creative events regresses infinitely. The evangelist precludes this theoretical possibility by his expression “in the beginning,” when only God and the divine Logos exist. Still the point remains that while for every thing that has come into being, there is a time in the past at which it began, nevertheless that does not imply that there is a time in the past at which everything began.
This implication reinforces the point which we have elsewhere made that the biblical concept of creation is an inherently temporal notion (Paul Copan and William Lane Craig, Creation out of Nothing: A Biblical, Philosophical, and Scientific Exploration [Grand Rapids, Mich.: Baker Bookhouse, 2004], chaps. 1-4). N.B. that to say that everything other than God has a temporal beginning is not to say that there is a temporal beginning of all things collectively. Theoretically, the sequence of past events could be enumerated by the negative numbers, beginning with the present event as 0, so that while everything that exists has individually a moment of its creation at some time in the finite past, nevertheless the series of creative events regresses infinitely. The evangelist precludes this theoretical possibility by his expression “in the beginning,” when only God and the divine Logos exist. Still the point remains that while for every thing that has come into being, there is a time in the past at which it began, nevertheless that does not imply that there is a time in the past at which everything began.
-
[3]
See the persistent misunderstanding of the question by my collaborators in Beyond the Control of God? Six Views on the Problem of God and Abstract Objects, ed. Paul Gould, with articles, responses, and counter-responses by K. Yandell, R. Davis, P. Gould, G. Welty, Wm. L. Craig, S. Shalkowski, and G. Oppy (Bloomsbury, forthcoming).
See the persistent misunderstanding of the question by my collaborators in Beyond the Control of God? Six Views on the Problem of God and Abstract Objects, ed. Paul Gould, with articles, responses, and counter-responses by K. Yandell, R. Davis, P. Gould, G. Welty, Wm. L. Craig, S. Shalkowski, and G. Oppy (Bloomsbury, forthcoming).
-
[4]
For references see Gregory E. Stirling, “‘Day One’: Platonizing Exegetical Traditions of Genesis 1:1-5 in John and Jewish Authors,” paper presented at the Philo section of the Society of Biblical Literature, San Antonio, Texas, November 20-23, 2004. The Logos appears already in the work of Antiochus of Ascalon and Eudores, two of the earliest Middle Platonists.
For references see Gregory E. Stirling, “‘Day One’: Platonizing Exegetical Traditions of Genesis 1:1-5 in John and Jewish Authors,” paper presented at the Philo section of the Society of Biblical Literature, San Antonio, Texas, November 20-23, 2004. The Logos appears already in the work of Antiochus of Ascalon and Eudores, two of the earliest Middle Platonists.
-
[5]
See Jutta Leonhardt-Balzer, “Der Logos und die Schöpfung: Steiflichter bei Philo (Op 20-25) und im Johannesprolog (Joh 1, 1-18)” in Kontexte des Johannesevangeliums, ed. Jörg Frey und Udo Schnelle, WUNT 175 (Tübingen: Mohr Siebeck, 2004), p. 318.
See Jutta Leonhardt-Balzer, “Der Logos und die Schöpfung: Steiflichter bei Philo (Op 20-25) und im Johannesprolog (Joh 1, 1-18)” in Kontexte des Johannesevangeliums, ed. Jörg Frey und Udo Schnelle, WUNT 175 (Tübingen: Mohr Siebeck, 2004), p. 318.
-
[6]
D. T. Runia, Philo of Alexandria and the “Timaeus” of Plato (Amsterdam: Free University of Amsterdam, 1983), pp. 140-3; Stirling, “ ‘Day One’.”
D. T. Runia, Philo of Alexandria and the “Timaeus” of Plato (Amsterdam: Free University of Amsterdam, 1983), pp. 140-3; Stirling, “ ‘Day One’.”
-
[7]
On the Cherubim [De cherubim]125-7. References to the Logos as the instrumental cause of creation are prevalent in Philo. Runia provides the following list: On the Creation of the World [De opificio mundi]; Allegorical Interpretation [Legum allegoriae] 3. 9; On the Cherubim 28; On the Sacrifices of Abel and Cain [De sacrificiis Abelis et Caini] 8; On the Unchangeableness of God [Quod Deus sit immutabilis] 57; On the Confusion of Tongues [De confusione liguarum] 62; On the Migration of Abraham [De migrationi Abrahami] 6; On Flight and Finding [De fuga et inventione] 12; 95; On Dreams 2.45; The Special Laws [De specialibus legibus] 1.81.
On the Cherubim [De cherubim]125-7. References to the Logos as the instrumental cause of creation are prevalent in Philo. Runia provides the following list: On the Creation of the World [De opificio mundi]; Allegorical Interpretation [Legum allegoriae] 3. 9; On the Cherubim 28; On the Sacrifices of Abel and Cain [De sacrificiis Abelis et Caini] 8; On the Unchangeableness of God [Quod Deus sit immutabilis] 57; On the Confusion of Tongues [De confusione liguarum] 62; On the Migration of Abraham [De migrationi Abrahami] 6; On Flight and Finding [De fuga et inventione] 12; 95; On Dreams 2.45; The Special Laws [De specialibus legibus] 1.81.
-
[8]
Runia, Plato and the “Timaeus,” p. 68. The locus classicus of the distinction was Plato’s Timaeus 27d5-28a4, which is in turn cited by Apuleius De Platone et eius dogmate 193; Nichomachus Introductio arithmetica 1. 2. 1; Numenius fr. 7; Justin Martyr Dialogue with Trypho 3. 5; Sextus Empiricus Adversus mathematicos 7. 142.
Runia, Plato and the “Timaeus,” p. 68. The locus classicus of the distinction was Plato’s Timaeus 27d5-28a4, which is in turn cited by Apuleius De Platone et eius dogmate 193; Nichomachus Introductio arithmetica 1. 2. 1; Numenius fr. 7; Justin Martyr Dialogue with Trypho 3. 5; Sextus Empiricus Adversus mathematicos 7. 142.
-
[9]
None of Runia’s texts draws the distinction at issue as fundamentally intelligible vs. sensible; rather it is being vs. becoming. The problem with the former characterization of the distinction is that it seems to leave no place of immaterial concreta like intelligences, angels, or souls. Given that the intelligible realm exists in the mind of God, such beings cannot be classed as part of the intelligible realm. They must be part of the sensible realm, which is thus more accurately described as the realm of concrete objects subject to becoming.
None of Runia’s texts draws the distinction at issue as fundamentally intelligible vs. sensible; rather it is being vs. becoming. The problem with the former characterization of the distinction is that it seems to leave no place of immaterial concreta like intelligences, angels, or souls. Given that the intelligible realm exists in the mind of God, such beings cannot be classed as part of the intelligible realm. They must be part of the sensible realm, which is thus more accurately described as the realm of concrete objects subject to becoming.
-
[10]
Runia, Plato and the “Timaeus,” p. 138.
Runia, Plato and the “Timaeus,” p. 138.
-
[11]
Conventionalists like Rudolf Carnap held such questions to have no framework-independent answer because they are meaningless; metaontological anti-realists like Mark Balaguer take them to be meaningful but deny that such ontological disputes have objective answers. N.B. the distinction between ontological anti-realism, such as is featured in Fig. 1, and metaontological anti-realism. Penelope Maddy’s so-called arealism is really closer to pretense theory.
Conventionalists like Rudolf Carnap held such questions to have no framework-independent answer because they are meaningless; metaontological anti-realists like Mark Balaguer take them to be meaningful but deny that such ontological disputes have objective answers. N.B. the distinction between ontological anti-realism, such as is featured in Fig. 1, and metaontological anti-realism. Penelope Maddy’s so-called arealism is really closer to pretense theory.
-
[12]
Thomas Morris and Christopher Menzel are ambiguous in this regard; Paul Gould and Richard Davis maintain, confusedly, I think, that God creates abstract objects but that these are divine thoughts.
Thomas Morris and Christopher Menzel are ambiguous in this regard; Paul Gould and Richard Davis maintain, confusedly, I think, that God creates abstract objects but that these are divine thoughts.
-
[13]
Gottlob Frege, The Foundations of Arithmetic: A Logico-Mathematical Enquiry into the Concept of Number, trans. J. L. Austin, 2d rev. ed. (Evanston, Ill.: Northwestern University Press, 1968), §I. 7, pp. 8-11; §II. 26-7, pp. 34-8.
Gottlob Frege, The Foundations of Arithmetic: A Logico-Mathematical Enquiry into the Concept of Number, trans. J. L. Austin, 2d rev. ed. (Evanston, Ill.: Northwestern University Press, 1968), §I. 7, pp. 8-11; §II. 26-7, pp. 34-8.
-
[14]
Notably Alvin Plantinga, Brian Leftow, and Greg Welty.
Notably Alvin Plantinga, Brian Leftow, and Greg Welty.
-
[15]
Graham Oppy, “Response to Welty,” in Beyond the Control of God?
Graham Oppy, “Response to Welty,” in Beyond the Control of God?
-
[16]
C. S. Lewis, “Bluspels and Flalansferes: A Semantic Nightmare,” in Selected Literary Essays, ed. Walter Hooper (Cambridge: Cambridge University Press, 1979), p. 258.
C. S. Lewis, “Bluspels and Flalansferes: A Semantic Nightmare,” in Selected Literary Essays, ed. Walter Hooper (Cambridge: Cambridge University Press, 1979), p. 258.
-
[17]
Ibid., pp. 260-1.
Ibid., pp. 260-1.
-
[18]
Ibid., p. 264.
Ibid., p. 264.
-
[19]
Ibid.
Ibid.
-
[20]
Ibid., p. 265.
Ibid., p. 265.
-
[21]
Stephen Yablo, “A Paradox of Existence,” in Empty Names, Fiction, and the Puzzles of Non-Existence, ed. Anthony Everett and Thomas Hofweber (Stanford: Center for the Study of Language and Information, 2000), p. 291.
Stephen Yablo, “A Paradox of Existence,” in Empty Names, Fiction, and the Puzzles of Non-Existence, ed. Anthony Everett and Thomas Hofweber (Stanford: Center for the Study of Language and Information, 2000), p. 291.
-
[22]
Stephen Yablo, “Go Figure: A Path through Fictionalism,” in Figurative Language, ed. Peter A. French and Howard K. Wettstein, Midwest Studies in Philosophy 25 (Oxford: Blackwell, 2001), p. 85.
Stephen Yablo, “Go Figure: A Path through Fictionalism,” in Figurative Language, ed. Peter A. French and Howard K. Wettstein, Midwest Studies in Philosophy 25 (Oxford: Blackwell, 2001), p. 85.
-
[23]
Stephen Yablo, “Does Ontology Rest on a Mistake?” Proceedings of the Aristotelian Society (Supplement) 72 (1998): 229. Cf. idem, “Paradox of Existence,” pp. 304-5.
Stephen Yablo, “Does Ontology Rest on a Mistake?” Proceedings of the Aristotelian Society (Supplement) 72 (1998): 229. Cf. idem, “Paradox of Existence,” pp. 304-5.
-
[24]
Yablo, “Does Ontology Rest on a Mistake?,” pp. 255, 259.
Yablo, “Does Ontology Rest on a Mistake?,” pp. 255, 259.
-
[25]
Yablo, “Paradox of Existence,” p. 293. By “commitment” I think Yablo means to indicate one’s commitment to the existence of the thing. Indeed, he seems to mean “conscious commitment,” the opposite of simulation or make-believe. Cf. idem, “Does Ontology Rest on a Mistake?,” p. 250; idem, “The Myth of the Seven,” in Fictionalism in Metaphysics, ed. Mark Eli Kalderon (Oxford: Clarendon Press, 2005), p. 98.
Yablo, “Paradox of Existence,” p. 293. By “commitment” I think Yablo means to indicate one’s commitment to the existence of the thing. Indeed, he seems to mean “conscious commitment,” the opposite of simulation or make-believe. Cf. idem, “Does Ontology Rest on a Mistake?,” p. 250; idem, “The Myth of the Seven,” in Fictionalism in Metaphysics, ed. Mark Eli Kalderon (Oxford: Clarendon Press, 2005), p. 98.
-
[26]
Yablo, “Myth of the Seven,” p. 98.
Yablo, “Myth of the Seven,” p. 98.
-
[27]
Yablo, “Paradox of Existence,” p. 295.
Yablo, “Paradox of Existence,” p. 295.
-
[28]
It should be noted that Yablo has an idiosyncratic understanding of what a platonic object is. Objects are platonic relative to an area of discourse iff the discourse depends on how those objects behave yet the discourse is not really about those objects. For example, someone who expresses concern about the number of starving people in the world is concerned about people, not some abstract object. Platonic objects, Yablo says, whether abstract or not, are deducible by overly easy existence proofs. He gives the following illustrations of discovering unexpected objects in statements’ truth conditions:
the truth value of: is held to turn on:
argument A is valid the existence of countermodels
it is possible that B the existence of worlds
there are as many Cs as Ds the existence of 1-1 functions
there are over five Es the number of E’s exceeding five
he did it Fly the event of his doing it being F
there are Gs which BLAH there being a set of Gs which BLAH
she is H her relation to the property H-ness
The entities denoted by the italicized terms in the right-hand column are platonic because the sentences in the left-hand column are not really about them (Yablo, “Paradox of Existence,” p. 277). The expressions on the right are therefore existential metaphors. If the objects denoted by such expressions do exist, most of them are plausibly construed to be abstract objects. In fact, Yablo himself says, “the existence of abstract objects is straightforwardly deducible from premises that few would think to deny” (Ibid., p. 276). Since our interest is in the existence of abstract objects, we shall take Yablo’s platonic objects to be abstract. Yablo notes that in addition to the parallels between figurative language and talk of platonic objects, evidence for the metaphorical character of such talk is that it is the best explanation of why such overly easy existence proofs fail.
It should be noted that Yablo has an idiosyncratic understanding of what a platonic object is. Objects are platonic relative to an area of discourse iff the discourse depends on how those objects behave yet the discourse is not really about those objects. For example, someone who expresses concern about the number of starving people in the world is concerned about people, not some abstract object. Platonic objects, Yablo says, whether abstract or not, are deducible by overly easy existence proofs. He gives the following illustrations of discovering unexpected objects in statements’ truth conditions:
the truth value of: is held to turn on:
argument A is valid the existence of countermodels
it is possible that B the existence of worlds
there are as many Cs as Ds the existence of 1-1 functions
there are over five Es the number of E’s exceeding five
he did it Fly the event of his doing it being F
there are Gs which BLAH there being a set of Gs which BLAH
she is H her relation to the property H-ness
The entities denoted by the italicized terms in the right-hand column are platonic because the sentences in the left-hand column are not really about them (Yablo, “Paradox of Existence,” p. 277). The expressions on the right are therefore existential metaphors. If the objects denoted by such expressions do exist, most of them are plausibly construed to be abstract objects. In fact, Yablo himself says, “the existence of abstract objects is straightforwardly deducible from premises that few would think to deny” (Ibid., p. 276). Since our interest is in the existence of abstract objects, we shall take Yablo’s platonic objects to be abstract. Yablo notes that in addition to the parallels between figurative language and talk of platonic objects, evidence for the metaphorical character of such talk is that it is the best explanation of why such overly easy existence proofs fail.
-
[29]
Yablo, “Paradox of Existence,” pp. 302-4; cf. idem, “Go Figure,” pp. 89-90; Stephen Yablo, “Abstract Objects: A Case Study, “in Realism and Relativism, ed. Ernest Sosa and Enrique Villaneva, Philosophical Issues 12 (Boston: Blackwell, 2002), pp. 227-30.
Yablo, “Paradox of Existence,” pp. 302-4; cf. idem, “Go Figure,” pp. 89-90; Stephen Yablo, “Abstract Objects: A Case Study, “in Realism and Relativism, ed. Ernest Sosa and Enrique Villaneva, Philosophical Issues 12 (Boston: Blackwell, 2002), pp. 227-30.
-
[30]
Gideon Rosen and John P. Burgess, “Nominalism Reconsidered,” in The Oxford Handbook of Philosophy of Mathematics and Logic, ed. Stewart Shapiro (Oxford: Oxford University Press, 2005), p. 533.
Gideon Rosen and John P. Burgess, “Nominalism Reconsidered,” in The Oxford Handbook of Philosophy of Mathematics and Logic, ed. Stewart Shapiro (Oxford: Oxford University Press, 2005), p. 533.
-
[31]
Burgess and Rosen themselves acknowledge that on Yablo’s view “an existence theorem is ambiguous between a literal and a figurative sense” (Rosen and Burgess, “Nominalism Reconsidered,” p. 528). I am not sure how seriously they take this ambiguity.
Burgess and Rosen themselves acknowledge that on Yablo’s view “an existence theorem is ambiguous between a literal and a figurative sense” (Rosen and Burgess, “Nominalism Reconsidered,” p. 528). I am not sure how seriously they take this ambiguity.
-
[32]
Yablo, “Go Figure,” p. 88; idem, “Paradox of Existence,” pp. 286-90.
Yablo, “Go Figure,” p. 88; idem, “Paradox of Existence,” pp. 286-90.
-
[33]
Yablo, “Myth of the Seven,” p. 99; idem, “Abstract Objects,” pp. 230-2. The real content of arithmetical truths like 2+3=5 is the first-order logical truth ($2xFx & $3yGy & Ø$z (Fz & Gz)) ®$5u(Fu v Gu). When it comes to non-numerical mathematical statements such as are comprised by set theory, Yablo takes the figurative language of sets to express certain combinatorial logical truths, that is, truths about what one gets when combining objects in different ways.
Yablo, “Myth of the Seven,” p. 99; idem, “Abstract Objects,” pp. 230-2. The real content of arithmetical truths like 2+3=5 is the first-order logical truth ($2xFx & $3yGy & Ø$z (Fz & Gz)) ®$5u(Fu v Gu). When it comes to non-numerical mathematical statements such as are comprised by set theory, Yablo takes the figurative language of sets to express certain combinatorial logical truths, that is, truths about what one gets when combining objects in different ways.

